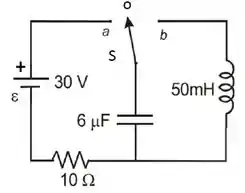
No circuito da figura ao lado, o capacitor está inicialmente descarregado e a corrente no indutor é nula. A chave está inicialmente na posição central ().
A chave passa então para a posição , onde permanece durante um tempo equivalente a duas constantes de tempo capacitivas. Em seguida (no novo instante de tempo ), passa para a posição , na qual permanece por um tempo muito longo.
- Determine a expressão da corrente que percorre o indutor em função do tempo. Qual é o valor da amplitude máxima da corrente?
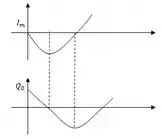
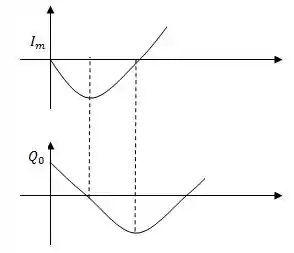
- Trace os gráficos das variações da corrente no indutor e da carga no capacitor em função do tempo quando a chave está na posição .
- Determine a energia total armazenada no circuito .
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Letra (a):
Quando a chave está na posição “a” temos um circuito , e para caracterizar esse circuito temos a constante :
E essa chave permanece nessa posição durante o tempo :
Então nesse tempo o capacitor se carrega com a carga que é dada pela seguinte expressão:
Temos que , então agora é só substituir:
Fazendo a aproximação que temos:
Quando a chave passa para a posição “b”, temos um circuito , onde o capacitor está carregado com a carga que a gente acabou de calcular:
A corrente do circuito varia de acordo com a seguinte expressão:
A frequência de oscilação é proporcional aos parâmetros do capacitor e do indutor:
E a amplitude máxima é:
Resumindo, a expressão completa da corrente em função do tempo é:
E a amplitude máxima é:
Passo 2
Letra (b):
Quando a chave está na posição “b” a carga é máxima e tem valor igual a , já a corrente tem seu valor mínimo. Ambas as quantidades oscilam no tempo: à medida que o tempo aumenta a carga vai diminuindo e a corrente aumenta em módulo, mas para o sentido negativo. Os gráficos ficam mais ou menos assim:
Tranquilo? Vamos para o último item?
Passo 3
Letra (c):
A energia total armazenada no circuito pode ser encontrada pela energia total ou do capacitor ou do indutor. A gente já sabe que funciona parecido com a energia mecânica em uma montanha russa: enquanto a energia do capacitor é máxima, a do indutor é mínima, e vice e versa. Mas sempre mantendo a energia total constante, claro=)
Então aqui vou usar a do capacitor, mas você pode conferir o resultado fazendo para o indutor e encontrar o mesmo resultado, beleza?
Beleza?
Pronto pra próxima questão? =)
Resposta