Uma corrente i percorre um fio muito longo. O fio está posicionado inicialmente de maneira vertical. Em certo ponto, realiza um loop circular de raio e retorna à mesma orientação vertical, como mostra a Figura 1. Embora extremamente próximos, não há contato entre os pontos inicial e final do loop.

Com relação ao ponto C marcado na figura, calcule, utilizando a lei de Biot-Savart explicitamente:

1. O vetor campo magnético devido ao loop.
2. o vetor campo magnético devido a cada uma das duas seções retas do fio

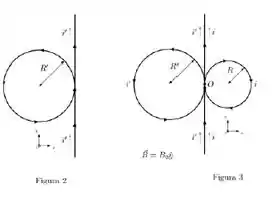
Considere agora outra configuração, onde uma nova corrente i’ percorre um segundo fio também muito longo. Mais uma vez, o fio está posicionado inicialmente de maneira vertical e, em certo ponto, realiza um loop circular de raio , retornado à mesma orientação vertical, como mostra a Figura 2. Embora extremamente próximos, não há contato entre os pontos inicial e final do loop.

Em seguida, esse fio é colocado bem próximo (mais uma vez, sem contato) ao primeiro fio, como mostra a Figura 3. No sistema descrito pela Figura 3, existe um campo magnético constante .

3. Qual deve ser a relação entre as correntes e para que o torque resultante devido ao campo magnético sobre o conjunto de loops seja nulo?

Letra (b):

Agora a distância não é mais constante, e podemos fazer um triângulo retângulo com a distância e o raio :

Já o ângulo entre o elemento de corrente e o vetor normal é:

Agora é só jogar isso na lei de Biot-Savart:

E consultando uma tabela de integrais temos:

Tranquilo? Vamos para o último item?

Letra (c):

Como nas seções retas a corrente e o campo magnético estão na mesma direção, a força resultante será nula. Logo, não haverá contribuições desses termos no torque.

A contribuição virá apenas das circunferências:

Da direita

E da esquerda:

E como o torque total deve ser nulo:

Beleza?

Pronto pra próxima questão? =)