PUC-RIO – Física 3 2020.1 – P2– Questão 3
Os quatro fios retos, infinitos e paralelos ao eixo estão dispostos nos vértices de um quadrado de lado e têm correntes de mesmo módulo. Os sentidos das correntes e as posições dos fios estão indicados na Figura. Determinar o vetor campo magnético total (devido a todos os fios) nos pontos:
- de coordenadas .
- de coordenadas .
-
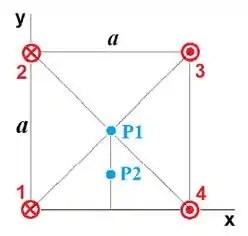
1,2 e sobre o fio .
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Letra (a):
Em todos os itens, vou usar a lei de ampere para determinar os campos. Como estamos falando de fios retilíneos, vou usar uma amperiana circular de raio e o campo fica assim:
Lembrando que todos os campos serão radiais e o sentido de cada um depende da orientação da corrente correspondente. Então agora precisamos analisar os campos em cada ponto. Vou fazer um esboço para ficar mais claro. Em relação ao ponto temos (usando a regra da mão direita pra achar o sentido de cada campo):
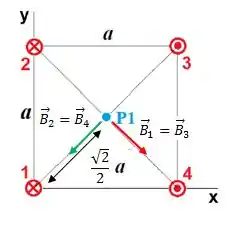
Por causa da simetria e da igualdade das intensidades das correntes, os campos e . E colocando a origem do sistema de coordenadas como no fio , a distância dos fios até o ponto é .
Então vamos calcular cada um separadamente, saca só:
E o campo resultante é a soma de todos os campos:
Passo 2
Letra (b):
Agora de forma similar os sinais dos componentes e dos campos são os mesmos, só falta recalcular as coordenadas, ou seja, a distância do novo ponto aos fios. Em relação a primeira dupla de campos: e , a distância em é e até é . Mas esse vetor deve ser unitário, então devemos dividir essas distâncias pelo valor da hipotenusa do triângulo formado por esses catetos:
E essa é a distância também. Então agora é só substituir:
Agora para os campos e , a distância horizontal é e a vertical é . E a hipotenusa agora vale . Os campos ficam:
E o campo total é a soma de todos os outros campos:
Tranquilo? Vamos para o último item?
Passo 3
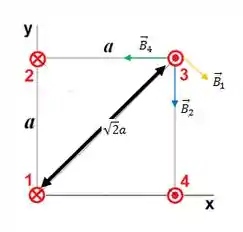Letra (c):
Deixa eu fazer um desenho pra facilitar as coisas:
O campo é:
O campo é:
O campo é:
E a resultante em é a soma desses campos:
E a força pode ser encontrada pelo produto vetorial do campo com o vetor na direção do fio (que no nosso caso é ):
E a força por unidade de comprimento é:
Beleza?
Pronto pra próxima questão? =)