PF de Probest da UFRJ - 2019.1

Sejam a média de uma amostra aleatória de dimensão extraída de uma população normal de valor esperado µ e variância , e a média de uma amostra aleatória de dimensão , independente da primeira, extraída de uma população normal de valor esperado µ e variância . Mostre que:

(a) Se é um estimador não viesado de µ.

(b) A variância do estimador em (a) é mínima quando

A quantidade de partículas emitidas por uma fonte radioativa durante um período de uma hora é uma variável aleatória de Poisson com parâmetro λ, a princípio desconhecido. Sabe-se que a probabilidade de nenhuma partícula ser emitida durante esse intervalo de tempo é de 0,00673.

(a) Em média, quantas partículas são emitidas por hora? Escreva também a expressão da função densidade de probabilidade de, o tempo em horas entre duas emissões consecutivas.

(b) Sabendo que em 20 minutos após uma emissão nenhuma outra partícula foi emitida, qual a probabilidade de que precisamos esperar mais meia hora pela próxima emissão?

(c) Sejam os números de partículas emitidas pela fonte ao longo das 24 horas de um determinado dia, e admita que as quantidades de partículas emitidas em horas distintas são independentes entre si. Qual é a probabilidade de, ao longo dessas 24 horas, observarmos a emissão de no máximo 100 partículas?

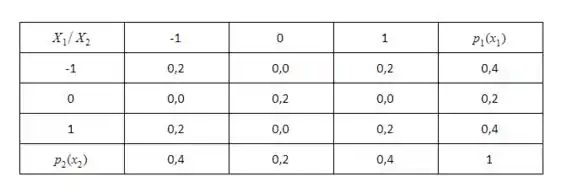Sejam (X1, X2) a variável aleatória bidimensional cuja distribuição conjunta é dada pela tabela:

(a) Calcule e , sendo.

(b) Calcule , e . As v.a.‘s e são independentes?

(c) O que se pode dizer sobre a veracidade da afirmação: "Se e são independentes, então "? Justifique.

(d) O que se pode dizer com relação a esta afirmação: "Se , então e são independentes"? Justifique

Em uma linha de produção, o engenheiro responsável pelo controle de qualidade deseja estimar a proporção de itens defeituosos produzidos. Para isso, seleciona aleatoriamente uma amostra de 50 itens, observando 4 itens defeituosos. Historicamente, mesmo em ocasiões de descontrole na linha de produção, a proporção de itens defeituosos jamais superou 15% e o engenheiro acredita que esse limiar continue a valer.

(c) Com base nos resultados experimentais calcule o p-valor correspondente ao teste da hipótese de que a proporção de itens defeituosos não supera 7% contra a alternativa de que supera 7%.

Em uma linha de produção, o engenheiro responsável pelo controle de qualidade deseja estimar a proporção de itens defeituosos produzidos. Para isso, seleciona aleatoriamente uma amostra de 50 itens, observando 4 itens defeituosos. Historicamente, mesmo em ocasiões de descontrole na linha de produção, a proporção de itens defeituosos jamais superou 15% e o engenheiro acredita que esse limiar continue a valer.

(b) Qual deve ser o tamanho de amostra coletada para que, ao se utilizar a proporção amostral de itens defeituosos como estimador da proporção de itens defeituosos na linha de produção, o erro absoluto de estimação seja inferior a 0,05, com probabilidade 95%?

Em uma linha de produção, o engenheiro responsável pelo controle de qualidade deseja estimar a proporção de itens defeituosos produzidos. Para isso, seleciona aleatoriamente uma amostra de 50 itens, observando 4 itens defeituosos. Historicamente, mesmo em ocasiões de descontrole na linha de produção, a proporção de itens defeituosos jamais superou 15% e o engenheiro acredita que esse limiar continue a valer.

(a) Construa um intervalo não conservativo ao nível de confiança 95% para a proporção de itens defeituosos na linha de produção.