Sabe-se que ocorre, em média, um acidente por dia numa certa estrada. Além disso, o número de ocorrências de acidentes ao longo de um intervalo de tempo de duração fixa segue uma distribuição de Poisson. Calcular a probabilidade de que:
- num determinado dia ocorressem pelo menos 3 acidentes. (calcule o resultado com 2 casas decimais);
- num grupo de 4 dias houvesse exatamente 2 dias, dos 4 selecionados, com pelo menos 3 acidentes por dia.
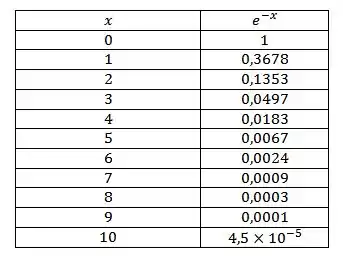
Obs.: Para simplificar os seus cálculos, use nas contas os valores (aproximados) que constam na tabela abaixo:
Passo 1
(a)
Pelo enunciado, a gente entende que temos, por exemplo:
E que em média ocorre 1 acidente por dia e que segue distribuição de Poisson, então:
Passo 2
Se ele quer a prob. de ocorrerem pelo menos 3 acidentes num dia, então ele quer.
Usando a fórmula de Poisson.
Passo 3
Substituindo os valores:
Passo 4
(b)
Primeira coisa que a gente tem que pensar é qual a prob. de ter 3 acidentes num dia.
Pelo cálculo da letra (a), a gente sabe que.
Isso será considerado como sucesso, ter pelo menos 3 acidentes no dia.
A gente terá um grupo de 4 dias,
E uma nova variável.
O que que isso lembra? Binomial, exato.
Passo 5
O exercício pede a prob. de dois dias acontecerem pelo menos 3 acidentes. Ele pede então.
Usando a fórmula da Binomial.