P1 de Probest da UFRJ - 2017.1

Três atiradores, Alberto, Bernardo e Carlos, atiram independentemente uma vez num alvo. Sabe-se que as probabilidades de acertar o alvo são 2/3 para Alberto, 3/4 para Bernardo e 1/2 para Carlos. Calcule a probabilidade

a) de que o alvo seja atingido;

b) de que somento um dos três acerte o alvo;

c) de no máximo um dos três acertar o alvo;

d) condicional de Alberto ter acertado dado que o alvo foi atingido por no máximo um dos três atiradores.

Todos os dias um técnico especializado em aparelhos de ar condicionado recebe chamados para atendimento domiciliar e, às vezes, ele leva consigo alguns auxiliares em todas as visitas do dia. Defina as variáveis aleatórias Y , número de atendimentos a fazer em um dia, e X, número de auxiliares que trabalham com ele naquele dia. A tabela a seguir apresenta a distribuição conjunta de X e Y .

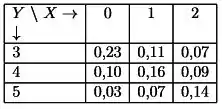
a) As variáveis X e Y são independentes? Justifique a resposta.

b) Calcule a probabilidade de X = k dado que Y = 5, para cada valor possível de X.

c) Calcule , ou seja, o número médio de auxiliares por atendimento.

Sabe-se que a duração em quilômetros rodados de pneus da marca A é normal. Um revendedor de pneus, para efeitos de garantia, quer calcular a probabilidade de que um pneu dessa marca dure mais de 55.000 quilômetros, mas não conhece os parâmetros média (µ) e desvio-padrão (σ) dessa distribuição normal. Com base em seus registros ele verificou que 21% desses pneus duram pelo menos 48.100 quilômetros; e 1% desses pneus dura no máximo 16.700 quilômetros.

a) Usando as informações do revendedor, calcule µ e σ.

b) Calcule a probabilidade de que um pneu da marca A dure mais do que 55.000 quilômetros.

Um aluno de educação física, conhecido na escola por ser “bom de pontaria”, é desafiado pelos amigos num jogo de basquete. O desafio consiste em fazer 20 lances livres de forma independente ao cesto de basquete e avaliar sua performance nessas jogadas. Sabe-se que em média a cada 20 lançamentos ele acerta 15. Com base nesta informação, responda as perguntas a seguir.

a) Calcule a probabilidade do aluno acertar ao menos 17 das 20 jogadas.

b) Calcule a variância do número de acertos ao cesto nas 20 jogadas.

c) O professor de basquete da escola decide entrar na brincadeira e fazer o desafio. Sabe-se que a probabilidade do professor errar o arremesso ao cesto é de 0,01. Usando a aproximação da Binomial pela Poisson, calcule a probabilidade do professor errar no máximo 2 vezes em 300 lançamentos ao cesto.