Sabe-se que a duração em quilômetros rodados de pneus da marca A é normal. Um revendedor de pneus, para efeitos de garantia, quer calcular a probabilidade de que um pneu dessa marca dure mais de 55.000 quilômetros, mas não conhece os parâmetros média (µ) e desvio-padrão (σ) dessa distribuição normal. Com base em seus registros ele verificou que 21% desses pneus duram pelo menos 48.100 quilômetros; e 1% desses pneus dura no máximo 16.700 quilômetros.
a) Usando as informações do revendedor, calcule µ e σ.
b) Calcule a probabilidade de que um pneu da marca A dure mais do que 55.000 quilômetros.
Passo 1
Sempre que estivermos em questões de normal, não pense duas vezes: desenhe! É a melhor forma de entender o problema.
Desenhando, teríamos isso:
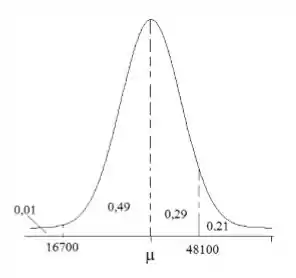
Nosso parâmetro é desconhecido, e sabemos que ele é o valor central.
Além disso, temos que marcar os valores que a questão deu pra gente. Ele fala que 1% dos pneus dura no máximo 16700 km, ou seja, a probabilidade até esse valor é 0,01. Depois disso, temos a informação que 21% dos pneus duram pelo menos 48100 km, então a probabilidade acima desse valor é 0,21.
Passo 2
a) Usando as informações do revendedor, calcule µ e σ.
Considerando nossa v.a. e pelo desenho que a gente acabou de fazer, sabemos que:
Porém, não podemos trabalhar com isso desse jeito: precisamos padronizar!
Assim, ficaríamos com:
Agora temos que ir lá na nossa tabela normal, e procurar qual valor me dá probabilidade 0,79. O valor que encontramos na tabela é aproximadamente 0,81. Ou seja:
Passo 3
Agora vamos repetir o mesmo passo a passo que fizemos anteriormente, só que olhando pro 16700.
Padronizando isso aí...
Só que aqui tem um bizu: nossa tabela não tem esse valor de 0,01 de probabilidade! Vamos inverter e pegar o complementar.
Agora sim, se formos na nossa tabela, o valor que nos dá 0,99 de probabilidade é o 2,33. Logo, temos que:
Passo 4
Ficamos então com o seguinte sisteminha:
Somando as duas equações, temos que:
E, temos que nosso vale 40000.
Passo 5
b) Calcule a probabilidade de que um pneu da marca A dure mais do que 55.000 quilômetros.
Ele quer basicamente essa probabilidade:
Precisamos só padronizar isso e resolver:
Resposta
a) e
b) 0,0668