Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Probabilidade Conjunta de V.A. Bidimensionais Discretas

Ver Teoria
Exercício 17123456789101112131415161819

Enunciado

P1-2017/1 UFRJ Questão 4

Todos os dias um técnico especializado em aparelhos de ar condicionado recebe chamados para atendimento domiciliar e, às vezes, ele leva consigo alguns auxiliares em todas as visitas do dia. Defina as variáveis aleatórias Y , número de atendimentos a fazer em um dia, e X, número de auxiliares que trabalham com ele naquele dia. A tabela a seguir apresenta a distribuição conjunta de X e Y .

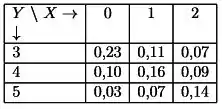
a) As variáveis X e Y são independentes? Justifique a resposta.

b) Calcule a probabilidade de X = k dado que Y = 5, para cada valor possível de X.

c) Calcule E X Y , ou seja, o número médio de auxiliares por atendimento.

Passo 1

a) As variáveis X e Y são independentes? Justifique a resposta.

Vamos ver se a função de probabilidade conjunta de X e Y fatora nas funções de probabilidade marginais.

Vamos escolher para análise P X = 0 , Y = 3 = 0,23 .

Pegando individualmente P ( X = 0 ) e P ( Y = 3 ) temos que:

P X = 0 = 0,36

P Y = 3 = 0,41

Fazendo P X = 0 ∙ P Y = 3 = 0,1476 ≠ 0,23 .

Logo, não são independentes!

Passo 2

b) Calcule a probabilidade de X = k dado que Y = 5, para cada valor possível de X.

Aqui ele quer basicamente a seguinte condicional:

P X = k Y = 5 = P ( X = k , Y = 5 ) P ( Y = 5 ) = P ( X = k , Y = 5 ) 0,24

Aqui vamos “travar” na linha Y = 5 , e ir substituindo os valores que P ( X ) pode assumir.

P ( k , 5 ) 0,24 = 1 8 ,     X = 0 7 24 ,     X = 1 7 12 ,     X = 2

Passo 3

c) Calcule E X Y , ou seja, o número médio de auxiliares por atendimento.

Aqui basicamente vamos fazer cada X Y e multiplicar pela sua probabilidade, e ir somando os resultados.

E X Y = ∑ x = 0 2 ∑ y = 3 5 x y p ( x , y ) = 0 + 1 3 ∙ 0,11 + 1 4 ∙ 0,16 + 1 5 ∙ 0,07 + 2 3 ∙ 0,07 + 2 4 ∙ 0,09 + 2 5 ∙ 0,14 ≈ 0,238

Resposta

a) Não

b) 1 8 , 7 24 , 7 12

c) 0,238

Exercícios de Livros Relacionados

Uma urna contém inicialmente 1 bola vermelha e 1 bola azul. Em cada rodada, uma bola é retirada aleatoriamente e substituída por duas outra bolas de mesma cor (por exemplo, se a bola vermelha ê a prim
Uma pilha do tipo C está em condição de trabalho com probabilidade 0,7 , enquanto uma pilha do tipo D está em condição de trabalho com probabilidade 0,4. Uma piIha é selecionada aleatoriamente de um c
Sorteiam-se bolas de uma urna que contém inicialmente 20 bolas vermelhas e 10 bolas azuis.(a) Qual é a probabilidade de que todas as bolas vermelhas sejam retiradas antes de todas as azuis?Agora supon
No Exemplo 3 f , suponha que a nova evidência esteja sujeita a possíveis interpretaçōes e de fato mostre que é apenas 90 % provável que o criminoso possua a característica em questão. Neste caso, qual
Suponha que 5 % dos homens e 0,25 % das mulheres sejam daltônicos. Uma pessoa daltônica é escolhida aleatoriamente. Qual é a probabilidade dessa pessoa ser um homem? Suponha que exista um mesmo número