P1 de Probest da UFRJ - 2018.2

O Chile encontra-se em uma das regiões do mundo que apresentam os maiores índices de ocorrência de terremotos. Suponha que o intervalo de tempo T entre a ocorrência de dois terremotos sucessivos possa ser modelado por uma variável aleatória exponencial com média desconhecida , em meses. Com base em dados históricos sabe-se que a probabilidade de que o intervalo de tempo entre dois terremotos exceda um ano é de 0, 001%.

(a) Usando a informação contida nos dados históricos, calcule o valor de λ e em seguida escreva a expressão matemática da função densidade de probabilidade da variável aleatória .

(b) Determine o número médio de terremotos no Chile durante um período de 6 meses e em seguida calcule a probabilidade de que nesse período de tempo ocorram no máximo dois terremotos.

(c) Um terremoto é considerado extremo se sua magnitude na escala Richter for superior a 10. Admitindo que a magnitude dos terremotos no Chile, na escala Richter, seja distribuída conforme uma normal de média 6,5 e desvio padrão 1, determine a probabilidade de um terremoto ser considerado extremo.

Um engenheiro apresentou orçamentos separados para a execução de uma obra num prédio em construção. O primeiro orçamento foi feito para a parte elétrica do prédio e o segundo orçamento foi feito levando em consideração a parte de encanamento do edifício. O engenheiro acha que a probabilidade de ganhar a concorrência da parte elétrica é de . Caso ele ganhe a parte elétrica, a chance de ganhar a parte de encanamento é de ; caso contrário, essa probabilidade é de . O engenheiro gostaria de saber qual a probabilidade:

(a) de ganhar o contrato referente à parte de encanamento;

(b) de ganhar os dois contratos;

(c) de ganhar apenas um contrato;

(d) condicional de ganhar o contrato da parte elétrica, dado que já ganhou o da parte de encanamento.

Suponha que o número de candidatos a participar em determinado curso seja uma v.a. cuja distribuição é uma Poisson com média de 4 inscrições. Se não houver um mínimo de 3 interessados o curso não será oferecido. Por outro lado, na sala há somente 5 computadores e, nas aulas, cada computador será utilizado por apenas um aluno. Calcule a probabilidade:

(a) de que haja mais interessados do que vagas;

(b) de que o curso não seja oferecido por escassez de inscrições (arredonde o resultado para 2 casas decimais);

(c) condicional de que todos os interessados consigam se inscrever dado que foi atingido o número mínimo de inscrições.

(d) de num ano em que houver 6 tentativas independentes de se oferecer este curso, em exatamente 2 delas o curso seja cancelado por escassez de inscrições.

Foi feito o loteamento de uma área rural em terrenos retangulares. Para cada terreno, seu comprimento e sua largura, ambos em metros, podem ser iguais a , ou . Para simplificar, vamos trabalhar em decâmetros (simbolicamente, ), lembrando que . Assim, tanto o comprimento como a largura de um terreno sorteado ao acaso, podem ser iguais a 1, 2 ou 3. A tabela a seguir fornece (apenas parcialmente) a distribuição conjunta de e , variáveis aleatórias supostas independentes:

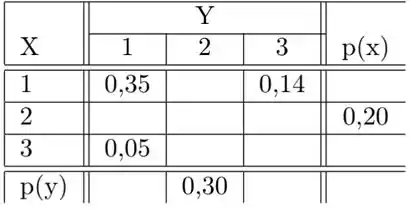
Considere as v.a.’s perímetro do terreno e área do terreno (em ).

Nessas condições, calcule:

(a) o valor de cada probabilidade, conjunta ou marginal, omitido na tabela acima.

(b) a probabilidade condicional de que a área seja igual a , dado que o perímetro é igual a .

(c) a média e a variância da área do terreno nesse loteamento.