Foi feito o loteamento de uma área rural em terrenos retangulares. Para cada terreno, seu comprimento e sua largura, ambos em metros, podem ser iguais a , ou . Para simplificar, vamos trabalhar em decâmetros (simbolicamente, ), lembrando que . Assim, tanto o comprimento como a largura de um terreno sorteado ao acaso, podem ser iguais a 1, 2 ou 3. A tabela a seguir fornece (apenas parcialmente) a distribuição conjunta de e , variáveis aleatórias supostas independentes:
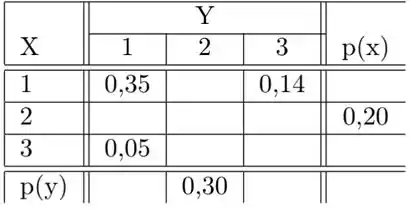
Considere as v.a.’s perímetro do terreno e área do terreno (em ).
Nessas condições, calcule:
(a) o valor de cada probabilidade, conjunta ou marginal, omitido na tabela acima.
(b) a probabilidade condicional de que a área seja igual a , dado que o perímetro é igual a .
(c) a média e a variância da área do terreno nesse loteamento.
Passo 1
a)
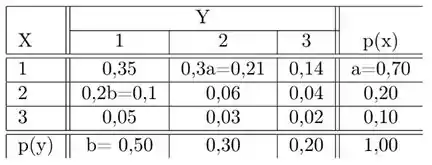
Para completar a tabela, temos que lembrar que essas variáveis são independentes, já que a largura e o comprimento podem assumir valores aleatórios sem terem relação entre si. Então:
Se supormos que , pela relação de independência:
Somando todos os elementos da linha e igualando a marginal temos:
Sabemos que a coluna das marginais de tem que somar , então:
Supondo agora que , pela independência, temos que:
Somando todos os elementos da linha e igualando a marginal :
Como sabemos que a coluna das marginais de também tem que somar 1:
Agora temos todas as marginais, e basta usarmos a relação de dependência entre elas para calcular o restante das probabilidades conjuntas:
Passo 2
b)
Queremos:
Substituindo as fórmulas das variáveis:
Agora temos que pensar, em que caso o perímetro é igual a e a área é igual a ? Resolvendo um sisteminha:
E quais os casos que
Possíveis valores de e :
ou
ou
Então nossa condicional fica:
Passo 3
c)
Agora queremos e . Para isso, precisamos calcular , . Temos que multiplicar cada probabilidade marginal pelos seus respectivos e :
E para o caso com as variáveis ao quadrado:
Como as variáveis são independentes:
E a mesma independência existe quando elas estão ao quadrado, então:
E a variância é dada por:
Substituindo os valores:
Resposta
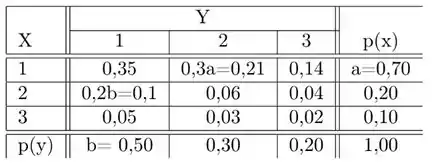
a)
b)
c)