P1 de Probest da UFRJ - 2020.2

A variável aleatória (v.a.) segue um modelo Binomial com parâmetros e .

a) Se e , calcule .

b) Se e , calcule o valor de .

c) Se e , calcule o valor de .

d) Se e , determine os valores de e .

Uma revista deseja estudar o comportamento do mercado brasileiro especificamente para clientes interessados em carros japoneses das marcas T Toyota), H (Honda) e N (Nissan). A compra do primeiro carro é feita com as probabilidades ; e . Um estudo sobre os hábitos de mudança de marca por parte dos usuários mostrou o seguinte quadro de probabilidades condicionais que prevalece em qualquer momento no qual um usuário típico adquire um novo automóvel:

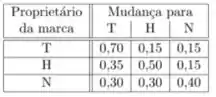
Por exemplo, representa mudança de um carro da marca Toyota no momento para outro carro Toyota no momento . Sendo assim, olhando na tabela, temos por exemplo , e para todo .

Quais são as probabilidades de que, para um tal cliente:

a) O segundo automóvel seja um Toyota, ou seja ? De que seja Honda, ou seja, ? De que seja Nissan, ou seja, ?

b) O terceiro automóvel seja um Toyota, ou seja, ?

c) O primeiro automóvel tenha sido um Toyota, dado que o segundo também foi da marca Toyota, isto é, ?

Suponha que o tempo em horas gasto com o reparo de um determinado tipo de máquina que tenha apresentado defeito seja uma variável aleatória exponencial de taxa (ou seja, média de horas).

a) Qual a probabilidade de que um reparo leve entre e horas para ser efetuado?

b) Suponha que esta máquina tenha defeito e esteja em reparo há horas. Calcule a probabilidade de que, ao longo das duas horas seguintes, a máquina esteja em processo de reparo.

c) Considere que o reparo de cada máquina desse tipo acarreta um custo fixo de reais por máquina mais um custo variável por máquina de reais/hora proporcional ao tempo em que máquina fique em reparo. Obtenha o valor esperado e o desvio padrão do custo total com reparos num mês em que 3 dessas máquinas apresentem falha, admitindo independência entre os tempos de reparo.

Admita que a largura dos ombros de pessoas é uma variável aleatória (v.a.) normal de média e desvio padrão de . Pretende-se dimensionar o corredor de uma casa, de forma a permitir a passagem de duas pessoas, de maneira confortável. Consideram-se satisfeitas as condições de conforto quando há uma folga de entre os ombros de duas pessoas e também entre os ombros e as paredes.

a) Qual a probabilidade de uma pessoa, escolhida ao acaso dessa população, ter a largura dos ombros maior que ?

b) Um projetista desenhou o corredor com de largura. Qual a probabilidade da passagem se dar de maneira confortável?

c) Que largura deve ter o corredor para permitir, em dos casos, a passagem de duas pessoas, de maneira confortável?