Uma revista deseja estudar o comportamento do mercado brasileiro especificamente para clientes interessados em carros japoneses das marcas T Toyota), H (Honda) e N (Nissan). A compra do primeiro carro é feita com as probabilidades ; e . Um estudo sobre os hábitos de mudança de marca por parte dos usuários mostrou o seguinte quadro de probabilidades condicionais que prevalece em qualquer momento no qual um usuário típico adquire um novo automóvel:

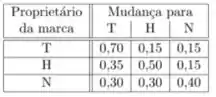
Por exemplo, representa mudança de um carro da marca Toyota no momento para outro carro Toyota no momento . Sendo assim, olhando na tabela, temos por exemplo , e para todo .

Quais são as probabilidades de que, para um tal cliente:

a) O segundo automóvel seja um Toyota, ou seja ? De que seja Honda, ou seja, ? De que seja Nissan, ou seja, ?

b) O terceiro automóvel seja um Toyota, ou seja, ?

c) O primeiro automóvel tenha sido um Toyota, dado que o segundo também foi da marca Toyota, isto é, ?

Fala galerinha, beleza? Bora resolver uma questão de prova!

O primeiro passo desse problema é extrair tudo que for possível da tabela! Pelo que foi apresentado no texto:

Essa são as probabilidades de transição, que nada mais são do que probabilidade condicionais. Se você já ouviu falar de cadeias de Markov, esse problema é exatamente sobre isso. Se você nunca ouviu falar disso, esquece isso que dá pra resolver o problema tranquilo também!

Para calcular a probabilidade do segundo carro ser da Toyota, basta considerar três casos: o primeiro é da Toyota e ocorre a transição de Toyota para Toyota, o primeiro é da Honda e ocorre a transição de Honda para Toyota, ou ainda, o primeiro é da Nissan e ocorre a transição de Nissan para Toyota. Para a probabilidade do segundo carro ser Nissan ou Honda, basta fazer as modificações nas transições que chegamos lá!

Com isso, podemos escrever:

Já sabemos que , , e as probabilidades de transição. Agora é só fazer conta. Mas eu quero discutir com vocês uma outra coisa muito legal! Se você não quiser ler o resto desse passo, sem problemas, pule pro passo 2.

Observe que a estrutura das equações acima lembra totalmente um produto de matrizes:

Repare que a matriz do meio é a matriz transposta da tabela, de modo que podemos escrevê-la como

Com isso, podemos sempre escrever:

Essa estrutura é típica das cadeias de Markov!