P2 de Probest da UFRJ - 2020.2

Suponha que o número de falhas de um determinado tipo de máquina ao longo de 10 anos de uso numa indústria seja uma variável aleatória que segue o modelo Poisson de taxa a ser estimada a partir de uma amostra aleatória de tamanho .

(a) Mostre que a média amostral é um estimador não viesado (não tendencioso) para .

(b) Utilizando a relação , calcule e .

(c) Considere agora o estimador para . Mostre que é viesado (viciado, tendencioso) e calcule seu viés (vício).

Foi realizado um procedimento de amostragem envolvendo a coleta de dados relativos a determinada população , que levaram à construção simultânea de dois intervalos de confiança: um deles para a média populacional da variável definida em (com base em uma amostra de tamanho nµ) e o outro para a proporção dos elementos de com certa característica (com base em uma amostra de tamanho np). Ocorre que, em todos os três itens a seguir, a razão entre a amplitude do intervalo de confiança e a estimativa pontual do parâmetro resultou ser exatamente a mesma, tanto no caso de se estimar como no caso de se estimar , ou seja,

(a) Calcule o valor da média amostral , se: (ou seja, se os níveis de confiança dos s˜ao iguais); (os tamanhos amostrais são iguais); , 2 (o desvio padrão populacional de X é ); (a proporção amostral é igual a ); e o para é não conservativo (não conservador).

(b) Determine o nível de confiança do para a proporção , se: ; a v.a. segue um modelo Normal; é desconhecido; (o coeficiente de variação amostral de é igual a ); (o nível de confiança do para é ); ; e o IC para é conservativo (conservador).

(c) Determine o tamanho de amostra usada para estimar se: ; ; o para é conservativo (conservador); (o coeficiente de variação populacional de é aproximadamente igual a ); (a média amostral está muito próxima da média populacional); e é conhecido.

Um economista tornou-se conhecido por sua capacidade de fazer predições de curto prazo bastante precisas sobre o comportamento futuro da economia nacional nas áreas: financeira, cambial, de comércio exterior, etc. Para avaliar sua capacidade preditiva, foram selecionadas 50 previsões feitas por ele em diferentes ocasiões ao longo do tempo, e relativas a importantes indicadores da conjuntura econômica nacional. Posteriormente, cada uma dessas previsões foi comparada com o valor que de fato ocorreu e verificou-se que, em desses casos o erro relativo da previsão foi menor que 10%. Com base nesses resultados, pretende-se testar a hipótese contra a alternativa , onde é a proporção populacional das vezes em que ele comete erros relativos menores que 10%.

(a) Qual é a sua conclusão ao nível de significância ?

(b) Determine todos os valores do nível de significância para os quais seria aceita e todos os valores de para os quais seria rejeitada, com base nos dados.

(c) Com o teste obtido em (a), qual seria a probabilidade de se cometer o Erro do Tipo II, se na verdade tivéssemos ?

Para estimar a magnitude da aceleração da gravidade G na superfície da Terra, realizou-se o seguinte experimento. Lançou-se uma bolinha de gude a partir do repouso 146 vezes a várias alturas diferentes com relação ao solo, anotando-se cada tempo ti , i ∈ {1, 2, . . . , 146} que a bolinha levou para tocar o chão. A partir do conjunto de observações dos pares altura e tempo até a bolinha atingir o solo, obteve-se uma amostra de medições para a aceleração da gravidade, calculadas em função dos valores de ti e medidos. A figura abaixo mostra o boxplot horizontal feito a partir das medições obtidas para G no experimento.

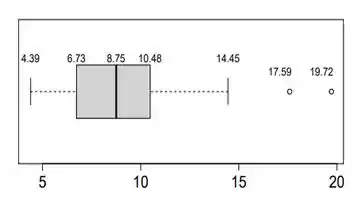
(a) Obtenha uma estimativa pontual para G com base no boxplot. Justifique.

(b) Dentre todas as medições obtidas na amostra, quantas se encontram entre e ? Justifique.

(c) Forneça as cercas do boxplot e, com elas, obtenha uma regra que permita classificar uma medição futura de G por esse experimento como outlier. A estimativa 14,56 seria considerada um outlier segundo essa regra? Por que?