UFRJ – Probabilidade e Estatística P2 – 2020/2 – Questão 1
Para estimar a magnitude da aceleração da gravidade G na superfície da Terra, realizou-se o seguinte experimento. Lançou-se uma bolinha de gude a partir do repouso 146 vezes a várias alturas diferentes com relação ao solo, anotando-se cada tempo ti , i ∈ {1, 2, . . . , 146} que a bolinha levou para tocar o chão. A partir do conjunto de observações dos pares altura e tempo até a bolinha atingir o solo, obteve-se uma amostra de medições para a aceleração da gravidade, calculadas em função dos valores de ti e medidos. A figura abaixo mostra o boxplot horizontal feito a partir das medições obtidas para G no experimento.
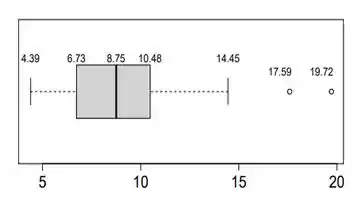
(a) Obtenha uma estimativa pontual para G com base no boxplot. Justifique.
(b) Dentre todas as medições obtidas na amostra, quantas se encontram entre e ? Justifique.
(c) Forneça as cercas do boxplot e, com elas, obtenha uma regra que permita classificar uma medição futura de G por esse experimento como outlier. A estimativa 14,56 seria considerada um outlier segundo essa regra? Por que?
Passo 1
a) Nessa primeira letra aqui, temos que determinar uma estimativa pontual para G com base no boxplot.
Como é uma estimativa pontual, né? A melhor medida possível é a mediana...
A mediana é adequada, porque é a medida de posição central que separa o conjunto de dados em duas regiões, ambas contendo a mesma quantidade de observações.
Passo 2
b) Em seguida, temos que encontrar quantas das medidas obtidas na amostra se encontram entre e ?
Bom! Até temos das medidas da amostra.
Logo, das medidas se encontram a direita de .
Isso quer dizer que descontando os dois outlier, que são e , teremos uma quantidade de medidas entre e , dadas por...
É isso aí, meus queridos! medidas entre e !
Passo 3
c)
Vamos calcular o comprimento do retângulo do boxplot...
Depois, o limite superior...
E por último, o limite inferior...
Valores fora do intervalo são considerados outliers. Logo, não seria considerado outlier.
Resposta