Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integral por Substituição – u=tg(x/2)

Ver Teoria
Exercício 61234578910

Enunciado

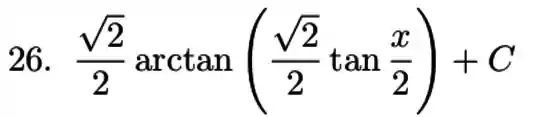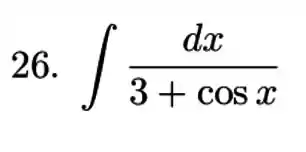
Passo 1

Para a nossa integral, vamos precisar das substituições

cos ⁡ x = 1 - z 2 1 + z 2

E

d x = 2 d z 1 + z 2  

Substituindo na integral

∫ d x 3 + cos ⁡ x = ∫ 1 3 + 1 - z 2 1 + z 2 2 d z 1 + z 2  

= ∫ 2 d z 3 ( 1 + z 2 ) + ( 1 - z 2 )

= 2 ∫ d z 3 + 3 z 2 + 1 - z 2

= 2 ∫ d z 4 + 2 z 2

= 2 ∫ d z 2 2 + z 2

= ∫ d z 2 + z 2

Passo 2

Ficou bem mais simples de resolver essa integral agora né? Vamos usar o método da substituição. Para usar esse método, vamos rearranjar nossa integral só mais um pouquinho.

∫ d x 3 + cos ⁡ x = ∫ d z 2 + z 2

= ∫ d z 2 z 2 2 + 1

= 1 2 ∫ d z z 2 2 + 1

Agora fazendo a substituição

u = z 2

d u = 1 2 d z

E aplicando na integral

1 2 ∫ d z z 2 2 + 1 = 1 2 ∫ 2 d u u 2 + 1

Sabemos que

∫ d u u 2 + 1 = arctan ⁡ u + C

Então ficamos com

∫ d x 3 + cos ⁡ x =   2 2 arctan ⁡ u + C

Desfazendo a substituição teremos

∫ d x 3 + cos ⁡ x =   2 2 arctan ⁡ z 2 + C

Passo 3

Maaaas, nossa variável não é z e sim x . Para desfazer aquela substituição inicial, precisamos lembrar que

z = tan ⁡ x 2

Então

∫ d x 3 + cos ⁡ x =   2 2 arctan ⁡ 1 2 tan ⁡ x 2 + C

∫ d x 3 + cos ⁡ x =   2 2 arctan ⁡ 2 2 tan ⁡ x 2 + C

Pronto! Esse método ajuda bastante!

Resposta

Exercícios de Livros Relacionados

5-18. Calcule a integral definida de duas formas: primeiro com uma substituição u na integral definida e, depois, com uma substituição u na integral indefinida.6. ∫ 1 2 4 x - 2 3 d x
Nos exercícios de 1 a 31, calcule a integral indefinida.17. ∫ d x s e n x + t g x
Nos exercícios de 1 a 31, calcule a integral indefinida.16. ∫ d x s e nx - c o s x + 2
O matemático alemão Karl Weierstrass (1815-1897) observou que a substituição t = t g x 2 converte qualquer função racional de s e nx e cos ⁡ x em uma função racional ordinária de t .c) Mostre que d x
Calcule as integrais usando uma substituição apropriada. ∫ e x 1 + e 2 xd x