Se e ,deduza as expressões para e .
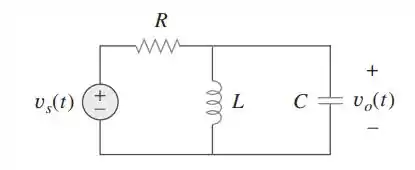
Passo 1
Aqui, vamos começar desenhando nosso circuito novamente no domínio da frequência e mostrando nossa tensão na forma fasorial. Perceba que o resistor continua sendo R, o indutor passa a ser e o capacitor passa a ser
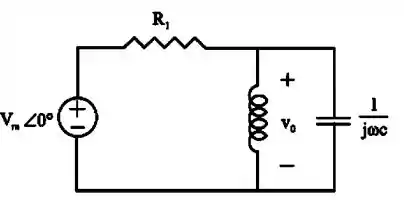
Passo 2
Agora, vamos calcular a impedância em paralelo:
Em seguida, a gente acha a nossa tensão que é aquela em cima do indutor (ou em cima do capacitor, as duas são iguais pois estão em paralelo)
Passo 3
Então, agora basta comparar com os dados do enunciado. Como temos , isso é a tensão que achamos só que no domínio do tempo. Se colocar no domínio da frequência, teremos .
Comparando…
Resposta
Exercícios de Livros Relacionados
O fasor corrente Ib, no circuito da Figura P9.36, é 25 ∠0 º º mA.. a) Determine Ia, Ic e Ig. b) Se v = 1.500 rad/s, determine as expressões para i a(t), i c (t) e i g(t).
No circuito da Figura 10.46, a corrente i(t) é: 10 cos tA b) 10 s e ntA c) 5 cos tA d) 5s e ntA e) 4.472 cos t - 63.43 ° A
Usando a Figura 10.51, elabore um problema para ajudar outros estudantes a entender melhor a análise nodal.
Use o PSpice ou MultiSim para determinar V o no circuito da Figura 10.124. Suponha v = 1r a d / s .
Usando a Figura 10.127 , elabore um problema para ajudar outros estudantes a entender melhor como realizar a análise C A com o PSpice ou MultiSim.