Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Leis de Kirchhoff para Corrente Alternada

Ver Teoria
Exercício 81234567910

Enunciado

Use análise de malhas para determinar v 0 no circuito abaixo. Seja v 1 = 120 cos ⁡ 100 t + 90 °   V e v 2 = 80 cos ⁡ 100 t   V

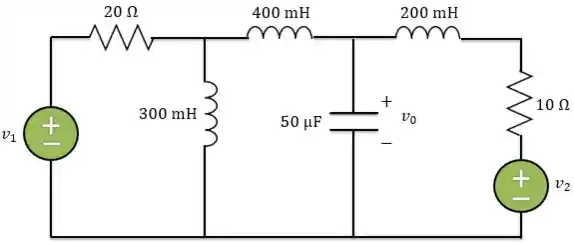
Passo 1

Primeiro, temos que passar o circuito para o domínio da frequência. Passando cada elemento, temos:

120 cos ⁡ ( 100 t + 90 ° )       →       120 ∠ 90 °   ,         ω = 100   r a d / s

80 cos ⁡ 100 t       →       80 ∠ 0 °   ,         ω = 100   r a d / s

400   m H       →       j ω L = j 40

300   m H       →       j ω L = j 30

200   m H       →       j ω L = j 20

50   µ F       →   -   j 1 ω C   = - j 200

Logo, o circuito no domínio da frequência é:

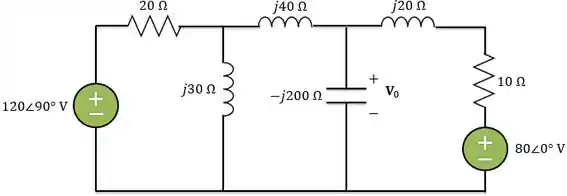
Passo 2

Agora, vamos preparar o circuito para utilizar a análise de malha:

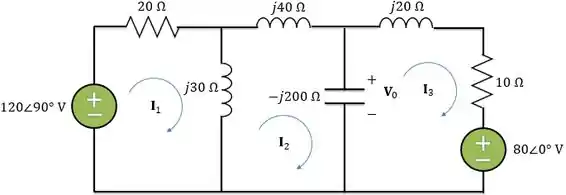
Pela lei de Ohm vemos que:

V 0 = - j 200 ( I 2 - I 3 )

Aplicando a LTK na malha 1:

- 120 ∠ 90 ° + 20 + j 30 I 1 - j 30 I 2 = 0

20 + j 30 I 1 - j 30 I 2 = j 120       ( i )

Aplicando a LTK na malha 2:

j 30 + j 40 - j 200 I 2 - j 30 I 1 - - j 200 I 3 = 0

- 30 I 1 - 130 I 2 + 200 I 3 = 0       ( i i )

Aplicando a LTK na malha 3:

- j 200 + j 20 + 10 I 3 - - 200 j I 2 + 80 ∠ 0 ° = 0

200 j I 2 + 10 - j 180 I 3 = - 80       ( i i i )

Passo 3

Então, precisamos resolver o sistema abaixo:

20 + j 30 I 1 - j 30 I 2 = j 120           ( i ) - 30 I 1 - 130 I 2 + 200 I 3 = 0               ( i i ) 200 j I 2 + 10 - j 180 I 3 = - 80   ( i i i )

Isolando I 1 na primeira equação, temos:

I 1 = j 120 + j 30 I 2 20 + j 30

I 1 = 120 ∠ 90 ° 36,05 ∠ 56,31 ° + 30 ∠ 90 ° 36,05 ∠ 56,31 ° I 2

I 1 = 3,33 ∠ 33,69 ° + 0,832 ∠ 33,69 °   I 2

Isolando I 3 na última equação, temos:

I 3 = - 80 - 200 j I 2 10 - j 180

I 3 = - 80 180,27 ∠ - 86,82 ° - 200 ∠ 90 ° 180,27 ∠ - 86,82 ° I 2

I 3 = - 80 180,27 ∠ - 86,82 ° - 200 ∠ 90 ° 180,27 ∠ - 86,82 ° I 2

I 3 = - 0,444 ∠ 86,82 ° - ( 1,11 ∠ 176,82 ° ) I 2

Substituindo I 1 e I 3 na equação ( i i ) , temos:

- 30 3,33 ∠ 33,69 ° + 0,832 ∠ 33,69 ° I 2 - 130 I 2 + 200 ( - 0,444 ∠ 86,82 ° - 1,11 ∠ 176,82 ° I 2 ) = 0

- 24,96 ∠ 33,69 ° I 2 - 130 I 2 - 222 ∠ 176,82 ° I 2 = 99,9 ∠ 33,69 ° + 88,8 ∠ 86,82 °

- 20,77 - j 13,84 - 130 + 221,66 - j 12,32 I 2 = 83,12 + j 55,41 + 4,93 + j 88,66

I 2 = 88,05 + j 144,07 70,89 - j 26,16

I 2 = 168,84 ∠ 58,57 ° 75,56 ∠ - 20,25 °

I 2 = 2,23 ∠ 78,82 °   A

Logo, na forma retangular I 2 será:

I 2 = 0,432 + j 2,187   A

Passo 4

Agora, vamos calcular I 3 utilizando o valor que encontramos para I 2 .

I 3 = - 0,444 ∠ 86,82 ° - ( 1,11 ∠ 176,82 ° ) I 2

I 3 = - 0,444 ∠ 86,82 ° - ( 1,11 ∠ 176,82 ° ) ( 2,23 ∠ 78,82 ° )

I 3 = - 0,0246 - j 0,443 - 2,475 ∠ 255,64 °

I 3 = - 0,0246 - j 0,443 + 0,614 + j 2,397

I 3 = 0,589 + j 1,954   A

Passo 5

Como já encontramos os valores de I 2 e I 3 , vamos substituí-los na equação abaixo:

V 0 = - j 200 ( I 2 - I 3 )

V 0 = - j 200 0,432 + j 2,187   - 0,589 + j 1,954

V 0 = - j 200 - 0,157 + j 0,233

V 0 = 200 ∠ - 90 ° 0,281 ∠ 123,97 °

V 0 = 56,2 ∠ 33,97 °   V

Passo 6

Para terminar, precisamos voltar para o domínio do tempo. Lembrando que ω = 100   r a d / s , temos:

v 0 t = 56,2 cos ⁡ 100 t + 33,97 °   V

Resposta

v 0 t = 56,2 cos ⁡ 100 t + 33,97 °   V

Exercícios de Livros Relacionados

O fasor corrente Ib, no circuito da Figura P9.36, é 25 ∠0 º º mA.. a) Determine Ia, Ic e Ig. b) Se v = 1.500 rad/s, determine as expressões para i a(t), i c (t) e i g(t).
No circuito da Figura 10.46, a corrente i(t) é: 10 cos ⁡ tA b) 10 s e ntA c) 5 cos ⁡ tA d) 5s e ntA e) 4.472 cos ⁡ t - 63.43 ° A
Usando a Figura 10.51, elabore um problema para ajudar outros estudantes a entender melhor a análise nodal.
Use o PSpice ou MultiSim para determinar V o no circuito da Figura 10.124. Suponha v = 1r a d / s .
Usando a Figura 10.127 , elabore um problema para ajudar outros estudantes a entender melhor como realizar a análise C A com o PSpice ou MultiSim.