Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Leis de Kirchhoff para Corrente Alternada

Ver Teoria
Exercício 21345678910

Enunciado

Determine i 0 no circuito abaixo usando a análise de malhas:

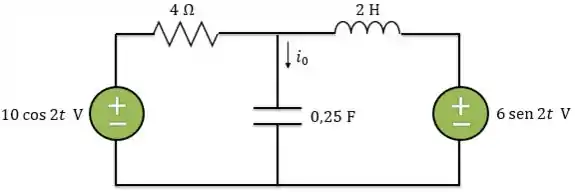
Passo 1

Primeiro, temos que passar o circuito para o domínio da frequência, ou seja, para forma fasorial. Como uma das fontes de tensão está expressa em seno, antes de passar para forma fasorial precisamos escrever em termos de cosseno:

6 sen ⁡ 2 t = 6 cos ⁡ ( 2 t - 90 ° )

Passando cada elemento, temos:

6 cos ⁡ ( 2 t - 90 ° )       →       6 ∠ - 90 °   ,         ω = 2   r a d / s  

10 cos ⁡ 2 t       →       10 ∠ 0 °   ,         ω = 2   r a d / s

2   H       →       j ω L = j 4

1   F       →   -   j 1 ω C   = - j 2

Logo, o circuito no domínio da frequência é:

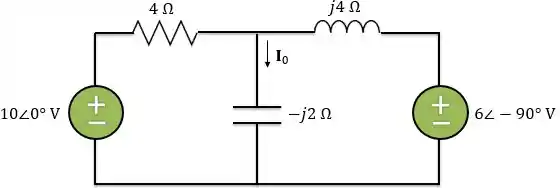
Passo 2

Agora, vamos preparar o circuito para utilizar a análise de malhas:

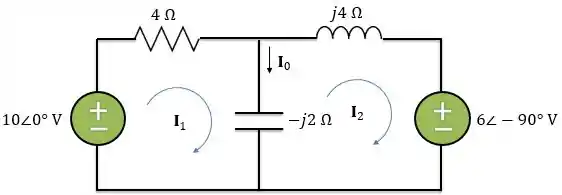
Aplicando a LTK na malha 1:

- 10 + 4 I 1 - j 2 I 1 - I 2 = 0

4 I 1 - j 2 I 1 + j 2 I 2 = 10

4 - j 2 I 1 + j 2 I 2 = 10

Agora, aplicando LTK na malha 2:

- j 6 - j 2 I 2 - I 1 + j 4 I 2 = 0

- j 2 I 2 + j 2 I 1 + j 4 I 2 = j 6

j 2 I 1 + j 2 I 2 = j 6

Dividindo toda equação por j 2 , temos:

I 1 + I 2 = 3

Passo 3

Chegamos a um sistema:

4 - j 2 I 1 + j 2 I 2 = 10 I 1 + I 2 = 3

Isolando I 2 na segunda equação e substituindo na primeira, temos:

4 - j 2 I 1 + j 2 ( 3 - I 1 ) = 10

4 - j 2 I 1 + j 6 - j 2 I 1 = 10

4 - j 4 I 1 = 10 - j 6

I 1 = 10 - j 6 4 - j 4

Passando para forma polar para efetuar a divisão:

I 1 = 11,66 ∠ - 30,96 ° 5,66 ∠ - 45 °

I 1 = 2,06 ∠ 14,04 °     A

Logo,

I 2 = 3 - I 1

I 2 = 3 - 2,06 ∠ 14,04 °

I 2 = 3 - ( 2 + j 0,5 )

I 2 = 1 - j 0,5     A

Analisando o circuito vemos que

I 0 = I 1 - I 2

Substituindo os valores que encontramos:

I 0 = 2 + j 0,5 - ( 1 - j 0,5 )

I 0 = 1 + j

I 0 = 1,414 ∠ 45 °     A

Passo 4

Agora é só voltar para o domínio do tempo. Lembrando que ω = 2   r a d / s , temos :

i t = 1,414 cos ⁡ 2 t + 45 °   A

Resposta

i t = 1,414 cos ⁡ 2 t + 45 °   A

Exercícios de Livros Relacionados

O fasor corrente Ib, no circuito da Figura P9.36, é 25 ∠0 º º mA.. a) Determine Ia, Ic e Ig. b) Se v = 1.500 rad/s, determine as expressões para i a(t), i c (t) e i g(t).
No circuito da Figura 10.46, a corrente i(t) é: 10 cos ⁡ tA b) 10 s e ntA c) 5 cos ⁡ tA d) 5s e ntA e) 4.472 cos ⁡ t - 63.43 ° A
Usando a Figura 10.51, elabore um problema para ajudar outros estudantes a entender melhor a análise nodal.
Use o PSpice ou MultiSim para determinar V o no circuito da Figura 10.124. Suponha v = 1r a d / s .
Usando a Figura 10.127 , elabore um problema para ajudar outros estudantes a entender melhor como realizar a análise C A com o PSpice ou MultiSim.