Determine no circuito abaixo:
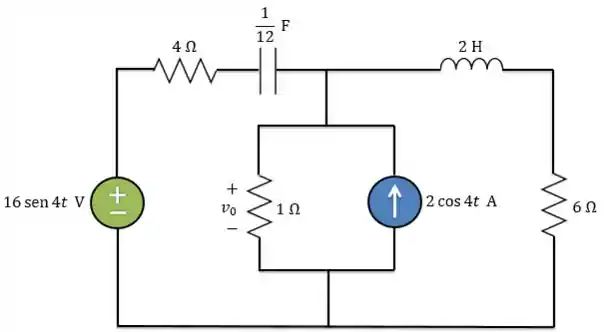
Passo 1
Primeiro, temos que passar o circuito para o domínio da frequência, ou seja, para forma fasorial. Como o a fonte de tensão está expressa em seno, antes de passar para forma fasorial precisamos escrever em termos de cosseno:
Passando cada elemento, temos:
Logo, redesenhando o circuito e passando para o domínio da frequência, temos:
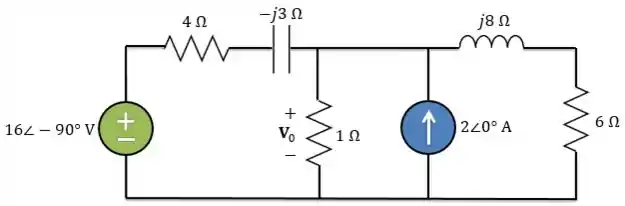
Passo 2
Agora, vamos preparar o circuito para utilizar a análise nodal:
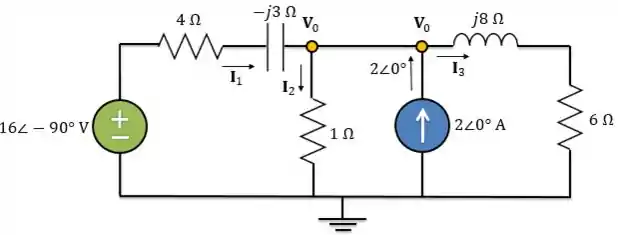Aplicando a LCK ao nó:
Como,
Substituindo,
Agora é só simplificar, para isso vamos precisar ficar passando os números complexos da forma polar para retangular e vice-versa.
Passo 3
Agora é só voltar para o domínio do tempo:
Resposta
Exercícios de Livros Relacionados
O fasor corrente Ib, no circuito da Figura P9.36, é 25 ∠0 º º mA.. a) Determine Ia, Ic e Ig. b) Se v = 1.500 rad/s, determine as expressões para i a(t), i c (t) e i g(t).
No circuito da Figura 10.46, a corrente i(t) é: 10 cos tA b) 10 s e ntA c) 5 cos tA d) 5s e ntA e) 4.472 cos t - 63.43 ° A
Usando a Figura 10.51, elabore um problema para ajudar outros estudantes a entender melhor a análise nodal.
Use o PSpice ou MultiSim para determinar V o no circuito da Figura 10.124. Suponha v = 1r a d / s .
Usando a Figura 10.127 , elabore um problema para ajudar outros estudantes a entender melhor como realizar a análise C A com o PSpice ou MultiSim.