Determine no circuito da Figura
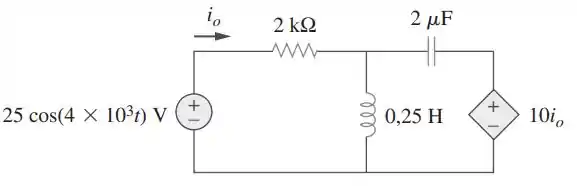
Passo 1
Vamos começar passando as nossas impedâncias para o domínio da frequência:
Analisando nossa fonte, vemos que
Para o indutor com indutância de :
)0.25
Para o capacitor com capacitância de :
Passo 2
Agora vamos redesenhar o circuito:
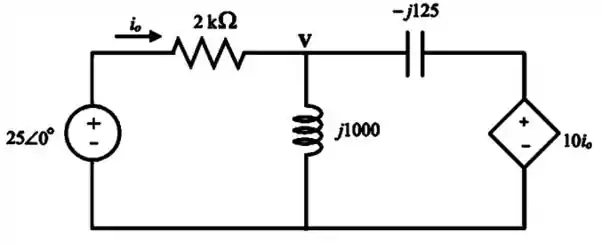
Passo 3
Vamos aplicar a Lei das Correntes de Kirchhoff ao nó V.
Passo 4
Agora, vamos calcular a corrente utilizando a Primeira Lei de Ohm: