Determine no circuito abaixo:
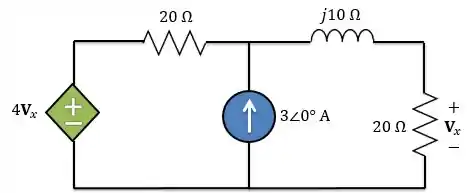
Passo 1
O circuito já está pronto para a gente trabalhar com fasores, pois já está no domínio da frequência. Além disso, precisamos determinar o fasor. Logo, nosso resultado final não precisará ser escrito no domínio do tempo.
Passo 2
Agora, vamos preparar o circuito para utilizar a análise nodal:
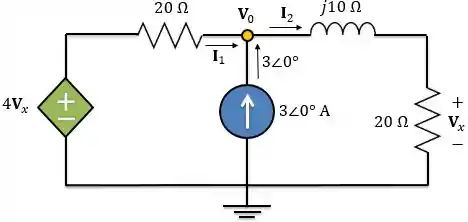
Aplicando a LCK ao nó:
Como,
Substituindo,
Passo 3
Precisamos encontrar mais uma equação que relacione e para podemos encontrar o que queremos. Para isso, vamos utilizar divisor de tensão:
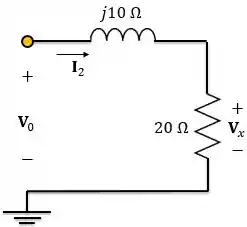
Logo,
Passo 4
Agora temos duas equações:
Substituindo em :
Passo 5
Agora, para terminar, precisamos deixar o fasor com módulo positivo. Para isso, basta subtrair ao ângulo: