Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Leis de Kirchhoff para Corrente Alternada

Ver Teoria
Exercício 71234568910

Enunciado

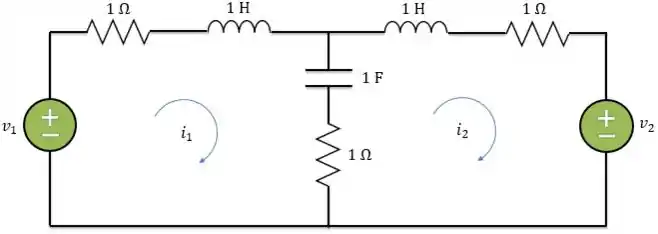
No circuito abaixo, determine as correntes de malha i 1 e i 2 . Seja v 1 = 10 cos ⁡ 4 t   V e v 2 = 20 cos ⁡ 4 t - 30 °   V .

Passo 1

Primeiro, temos que passar o circuito para o domínio da frequência. Passando cada elemento, temos:

10 cos ⁡ 4 t       →       10 ∠ 0 °   ,         ω = 4   r a d / s

20 cos ⁡ ( 4 t - 30 ° )       →       20 ∠ - 30 °   ,         ω = 4   r a d / s

1   H       →       j ω L = j 4

1   F       →   -   j 1 ω C   = - j 0,25

Logo, o circuito no domínio da frequência é:

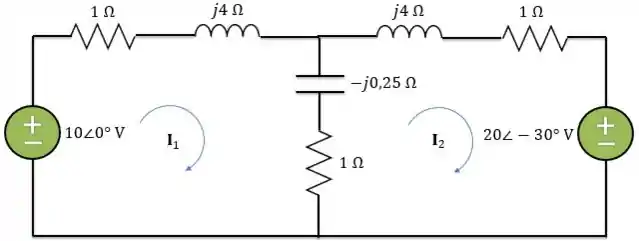
Passo 2

Aplicando a LTK na malha 1:

- 10 + I 1 + j 4 I 1 + 1 - j 0,25 I 1 - 1 - j 0,25 I 2 = 0

2 + j 3,75 I 1 - 1 - j 0,25 I 2 = 10

Aplicando a LTK na malha 2:

20 ∠ - 30 ° + 1 - j 0,25 I 2 - 1 - j 0,25 I 1 + 1 + j 4 I 2 = 0

- 1 - j 0,25 I 1 + 2 + j 3,75 I 2 = - 20 ∠ - 30 °

Passo 3

Então, precisamos resolver o sistema abaixo:

2 + j 3,75 I 1 - 1 - j 0,25 I 2 = 10 - 1 - j 0,25 I 1 + 2 + j 3,75 I 2 = - 20 ∠ - 30 °

Isolando I 1 na primeira equação, temos:

I 1 = 10 + 1 - j 0,25 I 2 2 + j 3,75  

I 1 = 10 + 1 - j 0,25 I 2 2 + j 3,75

I 1 = 10 2 + j 3,75 + 1 - j 0,25 2 + j 3,75 I 2

I 1 = 10 4,25 ∠ 61,93 ° + 1,03 ∠ - 14,04 ° 4,25 ∠ 61,93 ° I 2

I 1 = 2,35 ∠ - 61,93 ° + ( 0,242 ∠ - 75,97 ° ) I 2

Substituindo na segunda:

- 1 - j 0,25 ( 2,35 ∠ - 61,93 ° ) + 0,242 ∠ - 75,97 ° I 2 + 2 + j 3,75 I 2 = - 20 ∠ - 30 °

( - 1,03 ∠ - 14,04 ° ) ( 2,35 ∠ - 61,93 ° ) + 0,242 ∠ - 75,97 ° I 2 + 2 + j 3,75 I 2 = - 20 ∠ - 30 °

- 2,42 ∠ - 75.97 ° + ( - 0,249 ∠ - 90 ° ) I 2 + 2 + j 3,75 I 2 = - 20 ∠ - 30 °

0,249 j + 2 + j 3,75 I 2 = - 17,32 - j 10 + 0,587 - j 2,35

I 2 = - 16,73 + j 7,65 2 + j 4

I 2 = 18,4 ∠ 155,43 ° 4,47 ∠ 63,43 °

I 2 = 4,12 ∠ 92 °     A

Passo 4

Substituindo o valor que encontramos para a corrente I 2 para encontrarmos I 1 , temos:

I 1 = 2,35 ∠ - 61,93 ° + 0,242 ∠ - 75,97 ° 4,12 ∠ 92 °

I 1 = 1,1 - j 2,07 + 0,99 ∠ 16,03 °

I 1 = 1,1 - j 2,07 + 0,95 + j 0,273

I 1 = 2,05 - j 1,797

I 1 = 2,73 ∠ - 41,24 °     A

Passo 5

Agora é só voltar para o domínio do tempo:

i 1 t = 2,73 cos ⁡ 4 t - 41,24 °   A

i 2 t = 4,12 cos ⁡ 4 t + 92 °   A

Resposta

i 1 t = 2,73 cos ⁡ 4 t - 41,24 °   A

i 2 t = 4,12 cos ⁡ 4 t + 92 °   A

Exercícios de Livros Relacionados

O fasor corrente Ib, no circuito da Figura P9.36, é 25 ∠0 º º mA.. a) Determine Ia, Ic e Ig. b) Se v = 1.500 rad/s, determine as expressões para i a(t), i c (t) e i g(t).
No circuito da Figura 10.46, a corrente i(t) é: 10 cos ⁡ tA b) 10 s e ntA c) 5 cos ⁡ tA d) 5s e ntA e) 4.472 cos ⁡ t - 63.43 ° A
Usando a Figura 10.51, elabore um problema para ajudar outros estudantes a entender melhor a análise nodal.
Use o PSpice ou MultiSim para determinar V o no circuito da Figura 10.124. Suponha v = 1r a d / s .
Usando a Figura 10.127 , elabore um problema para ajudar outros estudantes a entender melhor como realizar a análise C A com o PSpice ou MultiSim.