Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lentes Delgadas

Ver Teoria
Exercício 81234567910111213141516171819

Enunciado

Na figura abaixo uma caixa se encontra sobre o eixo central da lente convergente delgada de algum ponto à esquerda da lente.

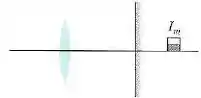
A imagem I m da caixa, produzida pelo espelho plano, que está 4,00   c m à direita do espelho. A distância entre a lente e o espelho é 10,0   c m , e a distância focal da lente é 2,00   c m .

a Qual é a distância entre a caixa e a lente?

A luz refletida pelo espelho atravessa novamente a lente e produz uma imagem final da caixa.

b Qual é a distância entre a lente e a imagem final?

Passo 1

a Qual é a distância entre a caixa e a lente?

Se a imagem da caixa está a 4,0   c m à direita do espelho plano, então a imagem gerada pela lente está a 4,0   c m à esquerda do espelho plano.

Logo, a imagem formada pela lente estará a uma distância i 1 da lente, dada por:

i 1 = 10 - 4 = 6,0   c m

Sabendo que a distância focal da lente é 2,0   c m , o objeto estará a uma distância p 1 da lente, dada por:

1 f 1 = 1 p 1 + 1 i 1

p 1 = i 1 × f 1 i 1 - f 1

Substituindo os valores, teremos:

p 1 = 6 × 2 6 - 2 = 3,0   c m

Passo 2

b Qual é a distância entre a lente e a imagem final?

Agora a imagem formada pelo espelho plano funciona com objeto. Dessa maneira, a distância entre o novo objeto e a lente será:

p 2 = 10 + 4 = 14   c m

Assim, a distância entre a lente e a imagem final será:

1 f 2 = 1 p 2 + 1 i 2

i 2 = p 2 × f 2 p 2 - f 2

Onde f 2 = f 1 = 2   c m . Logo:

i 2 = 14 × 2 14 - 2

i 2 = 2,33   c m

Resposta

a p 1 = 3,0   c m

b i 2 = 2,33   c m

Exercícios de Livros Relacionados

No método de Bessel para determinar a distância focal f de uma lente, um objeto e um anteparo estão separados por uma distância L , onde L4 f . É, então, possível, colocar uma lente entre o objeto e o
Obtenha a equação das lentes delgadas para uma lente de índice de refração n 2 situada entre dois meios de índices n 1 e n 3 . Verifique que o resultado se reduz ao que foi obtido, quando n 1 = n 3 .