Um objeto é colocado no centro de uma lente delgada e deslocado ao longo do eixo central. Durante o movimento a ampliação lateral é medida. A figura abaixo mostra o resultado em função da distância do objeto até .
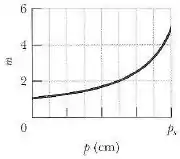
Determine a ampliação lateral do objeto para .
Passo 1
Vamos começar calculando a distância focal da lente.
Para isso, um bom ponto no gráfico para começarmos a trabalhar é o ponto cujas coordenadas são:
Logo:
Passo 2
A distância focal será:
Substituindo os valores, teremos:
Passo 3
A distância da nova imagem será:
Passo 4
A ampliação lateral desejada será dada por:
Resposta
Exercícios de Livros Relacionados
No método de Bessel para determinar a distância focal f de uma lente, um objeto e um anteparo estão separados por uma distância L , onde L4 f . É, então, possível, colocar uma lente entre o objeto e o
Obtenha a equação das lentes delgadas para uma lente de índice de refração n 2 situada entre dois meios de índices n 1 e n 3 . Verifique que o resultado se reduz ao que foi obtido, quando n 1 = n 3 .