Calcule os limites laterais de em , se .
Passo 1
Fala aii. Nossa função é uma função composta, pois depende de outra função, que é a . Já a função , por sua vez, é uma função dada por partes, pois dependendo do valor de ela assumirá uma forma diferente. Para valores de ela será , e se usaremos .
O que o enunciado nós pediu foi pra calcular os limites laterais quando . Então vamos começar escrevendo como fica a definição de de acordo com a :
Agora, vamos calcular os limites laterais que ele pediu fazendo as respectivas substituições e analisando os sinais.
Passo 2
Mas fica ligado numa coisa: quando , ou seja, , usaremos a primeira expressão para . Quando , ou seja, , usaremos a segunda expressão para beleza?
Show! Então no primeiro limite:
Da mesma forma que o primeiro, vamos substituir esse segundo limite lateral:
Substituições feitas! Agora só precisamos fazer a análise dos sinais.
Passo 3
Vamos começar no primeiro limite. Nesse caso, vou trazer o círculo trigonométrico para pensarmos sobre o sinal desse “infinito”, se é positivo ou negativo:
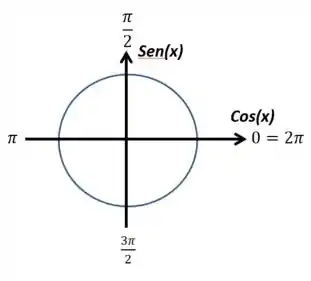
Repara que, para valores logo acima de (valores um pouquinho maiores que ), o seno é positivo, pois ficará na parte positiva do eixo do seno. Com isso:
Portanto,
Aqui nós não vamos escrever o no final porque ele vai ser um número muuuito pequeno quando comparado ao então podemos simplesmente desprezar. A única coisa que vai fazer diferença mesmo é o sinal.
Passo 4
Olhando para o mesmo desenho de antes, vamos reparar que o seno é negativo para valores logo antes de (valores pouco menores que ). Logo,
Portanto,
Repara que aqui também desprezamos o por ele ser desprezível ao comparado com o infinito.
Com isso encontramos nossos dois limites laterias.