Explique por que a função é descontínua no dado número . Esboce o gráfico da função.
Passo 1
Opaa, e ai!!!
O enunciado fornece uma função e um ponto e pede para justificarmos o motivo de não ser contínua nesse ponto.
Uma função é contínua em um ponto se ela estiver definida nesse ponto e, além disso, o valor da função neste ponto coincidir com o valor do limite. É isso que temos que verificar.
Passo 2
Para , a expressão da função é , que só não poderia ser utilizada exatamente em .
Assim, é bem definida em todos os pontos já que em ela é definida a parte a vale , de acordo com a nossa condição de baixo!
Então o domínio de é a reta real toda.
Passo 3
Show, mas ela ser definida não quer dizer que todos os nossos problemas estão resolvidos haha.
Vamos calcular o limite de quando tende a . Quando tomamos o limite, nos aproximamos de por valores de próximos de porém nunca iguais a .
Então, a expressão que devemos usar para o limite é , porque estamos usando números beeeem próximos de mas, ainda sim , que é a condição para usar essa expressão!
Passo 4
Vamos calcular os limites laterais.
O limite à esquerda é
O limite à direita é:
Os limites laterais são diferentes (logo o limite não existe) e diferem também do valor da função em ().
Por isso, não é contínua em .
Passo 5
O esboço do gráfico da função é:
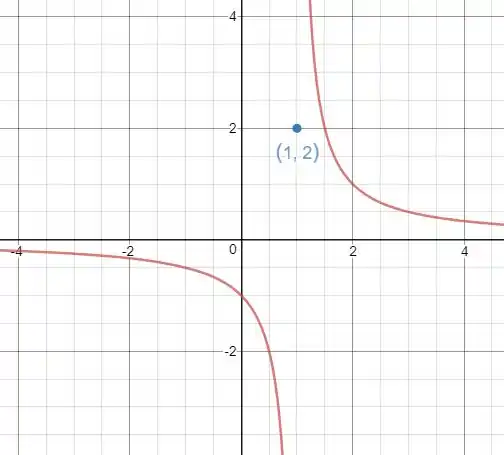
Resposta
Os limites laterais são diferentes (logo o limite não existe) e diferem também do valor da função em ().
Por isso, não é contínua em .