Resolva o seguinte limite:
Passo 1
Já entrou uma secante aqui no meio, ai ai ai ai... Mas relaxa que, antes de tudo, vamos lembrar o que é . A secante é basicamente dada por:
Tá, mas e esse ai? Aqui a gente vai usar o circulo trigonométrico, que tem a seguinte carinha:
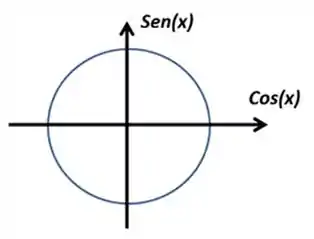
O círculo trigonométrico é basicamente um círculo de raio , e a partir dele vamos ter diferentes valores para as funções de ou dependendo do valor de beleza?
Aqui tem alguns principais valores de nos quais começamos marcando em 0 e vamos somando no senido anti-horário. Esses, são os valores de quando eles cruzam os eixos do seno e do cosseno. Vamos ficar com isso em mente!
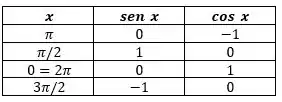
Passo 2
Agora voltando para o enunciado da questão, queremos encontrar:
Uma informação importante a ser dita, é que cada volta no círculo trigonométrico representa . Então alguns valores de apesar de serem diferentes vão representar a mesma coisa, pois damos voltas sobre os mesmo valores, como é o caso do quando adicionamos . Saca só:
Assim, o valor do seno e do cosseno de vai ser o mesmo que o de
Então, vamos substituir o na equação, ficando com:
Beleza, a gente já tem noção que isso vai dar . Resta saber como estamos nos aproximando de .
Passo 3
Pensando nessa análise do sinal, você percebe que a aproximação é feita pela esquerda, ou seja, para valores menores que .
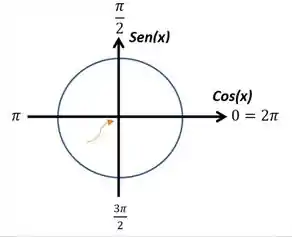
Bom, podemos ver que, quando está vindo por trás de , temos valores de cosseno negativo, pois ele está no eixo negativo do Dessa forma, podemos dizer que a aproximação se dará para . Portanto,