Explique por que a função é descontínua no dado número . Esboce o gráfico da função.
Passo 1
Faaaala aii! Bora continuar nosso estudo pra ficar fera em limites!
Bora começar lembrando o que é uma função contínua!
Uma função é contínua em um ponto se ela estiver definida nesse ponto e, além disso, o valor da função neste ponto coincidir com o valor do limite. Assim, devemos calcular tanto o limite como o valor da função em e compará-los.
Vamos calcular o limite de quando tende a . Quando tomamos o limite, nos aproximamos de por valores de próximos de porém nunca iguais a . Então, a expressão que devemos usar para o limite é .
Note que temos uma indeterminação do tipo . Ixi e agora?
Para eliminá-la, vamos fatorar o numerador e o denominador.
Para podemos colocar em evidencia, e ficamos com
Para temos uma diferença de quadrados
Que é
Que podemos escrever assim:
Passo 2
Reescrevendo nosso limite, temos:
Podemos simplificar o fator de modo que o limite fica
Shoow agora sumiu nossa indeterminação, podemos substituir!
Assim, encontramos nosso limite.
Agora temos que lembrar que , sendo assim a fução não é contínua em .
Passo 3
O esboço do gráfico da função é:
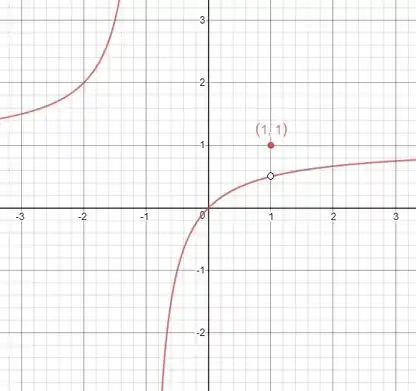
Resposta
A fução não é contínua em . E seu gráfico é: