Dadas as duas funções abaixo:
Calcule os limites laterais dados abaixo e verifique se o limite existe, comparando os limites laterais:
, , onde:
Passo 1
Opaaa, fala ai! Vamos continuar com nossos exercícios!
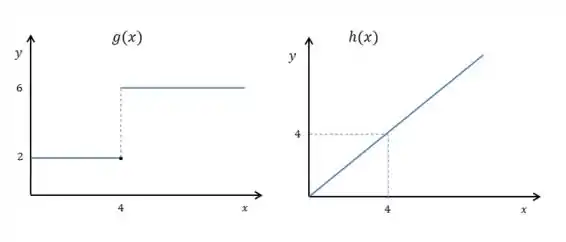
Bom, vamos primeiro escrever as leis das funções. Vamos começar por
A função é uma função com equação:
Já que:
Quando ,
Já a função é uma função constante dada por partes, descrita por:
Já que temos a reta quando e a reta quando
Passo 2
Show agora que já vimos bem quem são essas funções, vamos calcular os limites laterais delas!
Vamos calcular primeiro os limites laterais de por serem mais tranquilos:
Como essa função não tem probleminha, temos que os limites laterais são iguais, e é só substituir o valor!
Beleza, como você pode ver, eles são iguais.
Já a função vai precisar de uma atenção maior, a gente separou elas em duas partes né, para valores maiores que e para valores menores ou iguais a
Como o nosso limite lateral direito são valores um pouquinho maiores que , vamos usar a função , então temos que:
E, para o limite lateral esquerdo, temos valores um pouquinho menores que , então vamos usar a função , então o limite fica
Passo 3
Belezinha, agora que achamos os limites vamos relembrar uma coisinha.
Ele diz que
E, como ele quer os limites laterais de vamos fazer isso aqui:
E, para o limite esquerdo temos
Maaas em limites a gente tem uma propriedade que é: O limite do produto é igual o produto do limite. Então podemos usar os limites que acabamos de calcular. E fica exatamente assim:
Passo 4
Usamos ali a propriedade do limite de um produto. Agora é só a gente pegar os valores que calculamos:
E já achamos esses limites
Então temos que
Show! Matamos o limite da direita de
Passo 5
Agora vamos partir para o limite esquerdo!! Fazendo a mesma cois
E já achamos esses limites
Então temos que
Passo 6
Vimos então que os limites de são
Esses limites são diferentes, então dizemos que o limite não existe em
Resposta
E o limite não existe.