a) Do gráfico de , explique os pontos em que é descontínua e explique por quê.
b) Para cada um dos pontos indicados na parte (a), determine se é contínua à direita, à esquerda ou nenhum deles.
Passo 1
Vamos que vamos
A questão cobra de forma visual o conceito de continuidade.
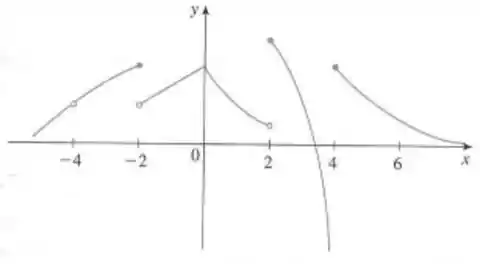
O enunciado nos dá o gráfico de uma função e pede, no item (a), para procurarmos os pontos em que não é contínua.
No item (b) é pedido para verificar se existem pontos de continuidade lateral.
É importante lembrar que uma função é contínua lateralmente em um ponto se um dos limites laterais de for igual ao valor da função naquele ponto.
Passo 2
Uma função contínua não tem buracos ou saltos.
Notemos que a função tem um buraco em e saltos em , e . Assim, não é contínua nesses pontos.
Então temos que não é continua em
Show! Matamos a letra
Passo 3
Agora vamos analisar esses pontos
Como é um ponto em que o gráfico de tem um buraco, a função não é contínua nem à direita nem à esquerda neste ponto.
Passo 4
Em , é contínua à esquerda pois o limite lateral à esquerda é igual ao valor da função, isto é,
Passo 5
Em , é contínua à direita pois o limite lateral à direita é igual ao valor da função, isto é,
Passo 6
O mesmo ocorre em . Em , é contínua à direita pois o limite lateral à direita é igual ao valor da função, isto é,
Resposta
a) , , e .
b) Contínua à direita: e .
Contínua à esquerda: .
Nenhuma delas: .