Considere a função definida pelo gráfico abaixo.
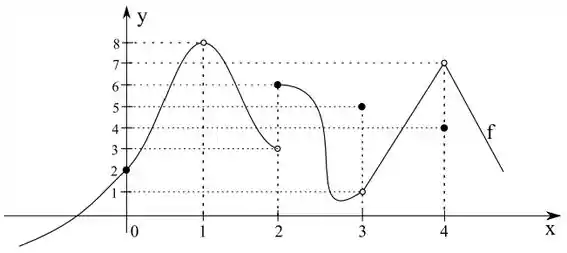
Determine o para se existir
Passo 1
Opa,tudo bom?? Vamos seguir com nossos estudos para aprender tudinho de limites laterais!
Vamos lembrar um pouco da teoria. Dizemos que um limite tem um certo valor , se
“E o que que isso quer dizer???” basicamente isso diz pra gente que o limite (que nesse caso vale ) existe se os limites laterais são iguais!
Então, o que teremos que fazer aqui é verificar os limites laterais em cada ponto.
Passo 2
Vamos começar com o ponto .
Se seguirmos o gráfico com o dedo pela esquerda até chegar a zero, vemos que:
Agora se fizermos a mesma coisa, seguir o gráfico com o dedo pela direita até chegar em zero, encontramos que
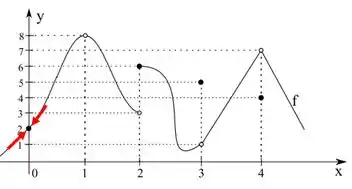
Ó que coisa boa, tanto pela esquerda quanto pela direita, o limite deu , isso quer dizer que o limite existe e vale
Passo 3
Vamos repetir para . Mas a função não está definida ali, já que temos uma bolinha aberta!!
Isso não importa, o limite só está interessado na tendência da função e não no valor no ponto. Então, pelo gráfico
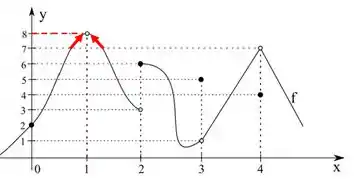
Assim,
Passo 4
Vamos repetir para . Aqui vamos analisar o gráfico com cuidado.
Se percorremos a função pela esquerda, temos que ao chegar em que está na altura então podemos concluir que
Agora, se formos pela direita, vamos chegar numa altura diferente, logo o limite pela direita é:
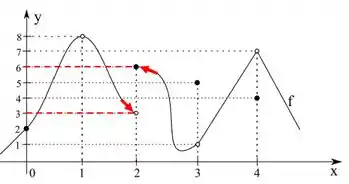
Pela definição que mostrei lá no passo 1, vemos que os laterais não batem. Então, o limite não existe.
Não existe
Passo 5
Vamos para o ponto . Vemos pelo gráfico que:
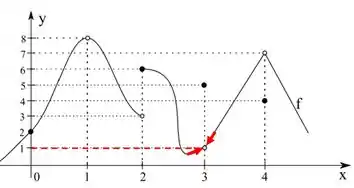
Assim,
Passo 6
Por último (ufa!), o ponto . Vemos pelo gráfico que:
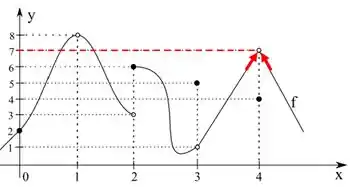
Assim,
Resposta
Não existe