Calcule os seguintes limites laterais:
Passo 1
Faaala aii, tudo show de bola?! Na hora de resolver um limite, normalmente,
substituímos o valor de da função pelo valor que ele está tendendo no limite, para termos uma ideia do que acontece. Fazendo isso aqui, ficamos com:
Putz, e agora? No caso dos limites laterais o buraco é mais em baixo, porque aqui quando o denominador se aproxima de zero, a fração tende para o infinito.
Mas afinal, qual é a resposta certa? Precisaremos analisar o limite para os dois casos, tanto quando quanto quando .
Passo 2
No caso dos limites laterais, vamos analisar o comportamento pelos dois lados do . Ou seja, vamos ver como a função se comporta quando se aproximar do pelo lado direito, tipo ou pelo lado esquerdo, tipo
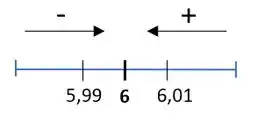
Isso faz com que o denominador resulte em algo um pouquinho maior ou um pouquinho menor que . Vamos olhar para um lado de cada vez.
Passo 3
Se a gente começar olhando para o lado esquerdo (), substituindo o temos:
E quanto mais eu me aproximar do menor esse número vai ficar:
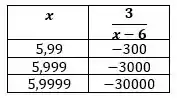
Até que ele se torne um infinito negativo!
Passo 4
Agora, substituindo pelo lado direito , por exemplo, com na função, ficamos com:
Repara que aqui quanto mais perto do eu chegar, menor vai ser o valor no denominador se aproximando do zero e fazendo com que a fração vá para o infinito, mas dessa vez positivo.
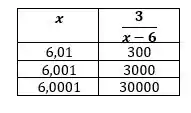
Logo, a diferença vai ser apenas no sinal.
Passo 5
Então, do lado direito tendemos para e do esquerdo . Ou seja,
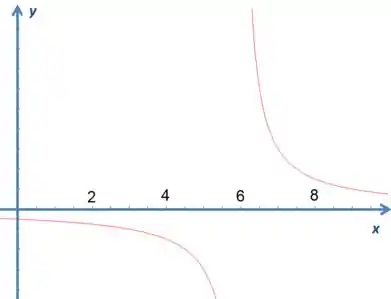
Ainda não acredita? Então dá uma olhada no gráfico: