Dado o . Considere e .
Encontre uma aproximação para usando o método de Euler Aperfeiçoado para cada .
Compare seus resultados com a solução exata dada por .
Passo 1
Temos o seguinte:
E com passo teremos o seguinte:
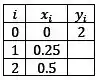
Aplicando a formuleta:
Iteração 1 :
Iteração 2 :
Logo, temos
Passo 2
Agora com :
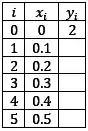
Iteração 1 :
Iteração 2 :
Iteração 3 :
Iteração 4 :
Iteração 5 :
E nossa aproximação aqui vai ficar:
Passo 3
A solução exata é:
Como podemos ver, ambas as nossas aproximações bateram com o valor exato da função naquele ponto. Isso pode ser explicado pela fórmula do erro! Temos:
Como nossa função é de segundo grau, sua derivada terceira é zero! Logo, o erro será zero independente do escolhido.
Resposta
Para , .
Para , .
O valor exato da função é . Logo, nossas aproximações bateram com o valor exato. Ver explicação acima.