Uma partícula 1, com massa de repouso nula e energia total move-se ao longo do eixo x e colide com outra partícula 2, com massa de repouso m e inicialmente em repouso. Após o choque, a partícula 1 inverte seu sentido do movimento e adquire energia total enquanto a partícula 2 é espalhada formando um ângulo com o eixo x.
(a) Encontre o ângulo de espalhamento .
(b) Calcule o vetor momento linear da partícula 2 após a colisão. Expresse suas respostas apenas em função de e
(c) Determine a expressão para apenas em função de e
Passo 1
Essa é uma questão clássica de colisão!
O que tá acontecendo é mais ou menos isso aqui:
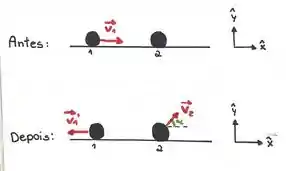
Vamos aplicar a conservação de energia antes e depois da colisão.
Antes das partículas colidirem, para a partícula 1 vamos ter a energia total e energia de repouso igual a 0, pois a massa de repouso dessa partícula é nula.
Além disso vamos ter a energia de repouso da partícula 2, dada por .
E depois da colisão?
Vamos ter a energia total da partícula 1, chamada de e a energia total da partícula 2, que vamos chamar de
Igualando essas duas quantidades:
Agora vamos fazer a mesma coisa para o vetor momento linear.
Lembra que:
Então como se trata de vetor, vamos dividir nas suas componentes x e y.
Para a componente x, antes de colisão temos somente momento linear para a partícula 1 (é a única que tem componente de velocidade nessa direção).
Usando a relação:
Podemos escrever para o momento linear em x da partícula 1:
Depois da colisão, como a partícula 1 inverte o sentido do seu movimento e tem energia total a componente de momento linear em x da partícula 1 vai ser dada por
Para a partícula 2, não sabemos quanto vale o momento linear depois da colisão, mas sabemos que sua componente x pode ser escrita como:
Então usando a conservação de momento linear em x:
Agora vamos ver a componente y do momento linear.
Antes da colisão, ela vale 0, pois a partícula 1 só tem velocidade em x e a partícula 2 se encontra parada.
Depois da colisão, a partícula 1 continua com movimento na direção do eixo x, então não vai contribuir para momento linear em y, mas não podemos afirmar o mesmo para a partícula 2.
Então vamos dizer que depois da colisão, a partícula 2 tem momento linear em y dado por:
Fazendo a conservação:
Passo 2
(a) Olha essa última equação que acabamos de escrever:
Como pois a partícula 2 se movimenta, então obrigatoriamente
Logo, ou
Mas, pela conservação do momento linear em x, o momento linear após a colisão deve continuar sento positivo.
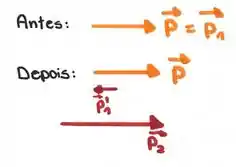
Por isso, e já que a partícula 1 se movimenta no sentido negativo do eixo x, partícula 2 deve se movimentar no sentido positivo de x e seu momento linear em x deve ser positivo.
Logo:
Por isso,
Passo 3
(b) Pela conservação do momento linear em x:
Como achamos que então e:
Como vimos que a componente em y do momento linear da partícula 2 após a colisão é nulo:
Podemos achar a energia total da partícula 2 através da equação de conservação de energia que escrevemos no Passo 1:
Passo 4
(c) Pela relação entre energia e momento linear relativístico:
Para a partícula 2 após a colisão, temos:
Substituindo os valores de e que achamos antes no Passo 3:
Para expandir o lado esquerdo, vamos lembrar que:
E vamos considerar e
Fazendo isso e simplificando:
Agora, pra simplificar esse lado direito, vamos lembrar que:
Então:
Resposta
(a)
(b) e
(c)