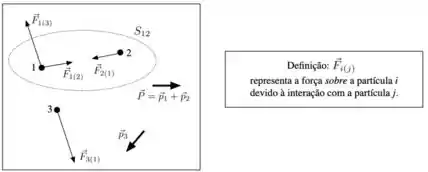
9) A figura mostra um sistema composto pelas partículas e , as quais interagem entre si através de forças atrativas. A partícula , externa ao sistema , interage repulsivamente com a partícula , mas não interage com a partícula . O momento linear total do sistema assim como o momento linear da partícula estão representados na figura. Admita, ainda, que o sistema esteja isolado da interação com outras partículas. Assinale a alternativa FALSA.
A)
B)
C)
D)
E)
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Nessa questão temos três partículas em que as partículas e interagem com uma força de atração entre elas, as partículas e interagem com uma força de repulsão e as partículas e não interagem entre sí.
Consideramos um sistema uma região que contém apenas as partículas e . E que o sistema esteja isolado.
Se e , qual das alternativas é falsa?
O que podemos fazer é analisar alternativa por alternativa e verificar se é verdadeira ou falsa, o que acha?
Mas antes, podemos evidenciar uma relação entre o momento linear e a força.
Dizemos que a variação do momento é igual a integral da força, ou seja
Derivando dos dois lados com relação a considerando e .
Ou seja, a derivada do momento de uma partícula será a soma das forças que agem sobre ela.
Entendeu essa parte? 😉
Bora lá!
Passo 2
Na alternativa A) diz que
O que acha? 👀
diz respeito ao momento linear do sistema como podemos ver na imagem do enunciado já que .
Como no sistema a força interna é ( e se cancelam) então a força resultante será a força que a partícula faz na partícula .
Então é correto dizer que a derivada do momento em é igual a força .
Logo, a alternativa A) é verdadeira.
Tranquilo até aqui? 😁

Passo 3
Analisando a alternativa B) que diz que .
Será mesmo? 🤔🤔
Essa alternativa nos diz que o momento linear em na partícula é apenas a resultante da força entre ela e a partícula .
Mas a partícula também não faz uma força na partícula ?
Portanto é errado dizer que o momento depende unicamente da força .
Logo, para essa alternativa estar correta, deveria ser
Entendeu?
Então, a alternativa B) é a alternativa falsa que procuramos!

Vamos continuar a analisar as outras para mostrar porque são verdadeiras.
Passo 4
A alternativa C) diz que
Já viu porque é verdadeira?
Como dizemos no passo a derivada do momento de uma partícula é igual as forças que atuam dobre essa partícula.
Como a partícula interage apenas com a partícula , seu momento certamente será igual a essa força de interação.
Então, a alternativa C) está correta!

Tranquilo? 😉
Passo 5
A alternativa D) diz que
Em outras palavras, a derivada do momento da partícula é igual a força que a partícula sofre da atração com a partícula .
Como a partícula interage apenas com a partícula é correto afirmar isso já que a força que atua na partícula é apenas .
Logo, a alternativa D) é verdadeira também!

Interessante, não é? 😁
Passo 6
Por fim, a alternativa E) diz que
Se é o momento linear do sistema e é o momento da partícula podemos englobar as três partículas em um único sistema e chamar de sistema .
No enunciado foi dito que está isolado de qualquer ação, ou seja, não há forças externas.
Em um sistema, a força interna resultante é , da mesma forma que vimos na alternativa A), lembra?
Assim, se não há forças resultantes no sistema , a variação do momento é igual a .
Então, a alternativa E) é verdadeira!
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍

Resposta
B)