6. Um pequeno drone está navegando numa dada altura constante quando, por causa de um defeito de fabricação, explode em dois fragmentos. Imediatamente após a explosão, verifica-se que um dos fragmentos com massa , move-se com velocidade e o outro fragmento, de massa , move-se com velocidade , ambas velocidades medidas no mesmo referencial inercial em repouso. A velocidade escalar do drone antes da explosão, em metros por segundo, medida no mesmo referencial inercial é:
Passo 1
E aí meus caros! Aqui, vamos nós resolver mais um probleminha dessa maravilhosa prova de Física.
E se liga só! Temos nas nossas mãos aí mais um probleminha sobre conservação de momento linear.
A questão fala pra gente que um drone está navegando numa dada altura, quando por um infortúnio do destino, acaba explodindo e se fragmentando em dois pedaços, cada um com uma velocidade.
Ora bolas! Temos então, desse modo, dois momentos pra analisar, o antes da explosão e o depois da explosão. Você aí, estudante, já deve tá se contorcendo pra igualar o momento antes e depois, multiplicar massa por cada velocidade correspondente, descobrir a velocidade antes da explosão e aí, só partir pro abraço. Afinal, tempo é o que a gente menos tem uma prova!
Mas calma, jovem! Não é assim que funciona! Alguns professores são de boas! Outros já são um pouquinho mais rígidos, hein!?
Antes de fazer o memorial de cálculo, tem uma coisa muito importante pra se fazer! É importante definir as condições que permitem que nosso sistema esteja sujeito à conservação!
E pra que isso aconteça, temos que considerar que, no instante da explosão, as forças internas ao sistema são muito maiores que as forças externas (peso e sustentação). Isso é o que garante que nossos sistema esteja bem isolado, e portanto, sujeito à conservação de momento!
Faz isso, viu! Os professores de Física variam quem corrige as provas! Vai que sua prova aí, cai nas mãos de um corretor durão!
Passo 2
Bom! Como já foi dito, bora utilizar a lei da conservação do momento linear:
Uma coisa importante aqui, é que o drone movimenta-se em uma altura constante antes da colisão, de modo que a componente vertical do momento linear será nula . Se não entendeu, se liga na imagem abaixo:
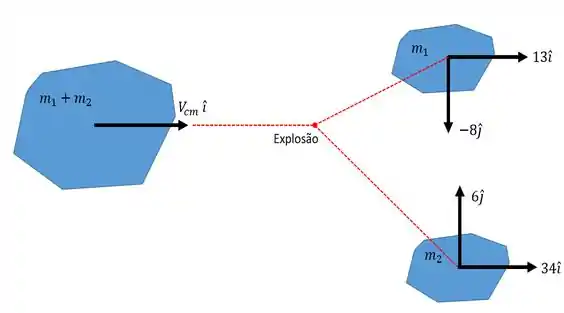
Com isso, temos que o momento antes vai ser:
Já o momento depois :
Igualando os dois momentos, como combinado:
Passo 3
Agora vem a coisa mais importante! Se liga só no macete! Antes da colisão, o drone só tinha componente de velocidade no eixo , certo!? Ou seja, só tinha momento em .
Isso quer dizer que após a colisão, o drone continuará tendo momento resultante apenas em ; de modo que a seguinte expressão abaixo precisa ser igual a zero:
Isolando :
E se vale zero, então a expressão que encontramos no final do fica:
Isolando :
E substituindo o valor de encontrado antes:
Finalmente encontramos nossa resposta!
Bola pra frente, que atrás vem gente!