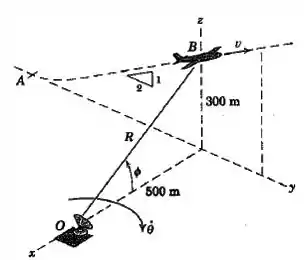
Uma aeronave decola em e se eleva em um ângulo constante com inclinação de para no plano vertical com uma velocidade constante . A aeronave é rastreada por radar em . Para a posição , determine os valores de , e .
Passo 1
Bom, vamos primeiro desenhar esse sistema mostrando as variáveis pertinentes:
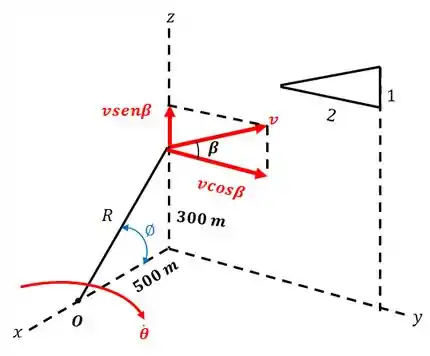
é o ângulo que o avião faz com a horizontal. Ele vale:
E
Usamos os dois triângulos da figura.
Passo 2
Para acharmos , primeiro decompomos usando (assim obtemos a velocidade vertical):
Após isso, decompomos na direção de
Ou seja:
Assim:
Pra achar , temos duas formas: primeiro usando a fórmula e segundo percebendo que a velocidade horizontal em é a própria
Percebeu? É só ver que ela tem uma tendência a girar ao redor do eixo central. Sendo assim:
Onde é o raio de giração.
Opa! Sacou o motivo de eu ter dividido o por Para transformar pra . Queremos achar , que é dada em . Assim:
Passo 3
Agora pra achar vamos seguir o mesmo procedimento: A velocidade seguindo a direção do ângulo pode ser dada por:
Ou, se você perceber, essa velocidade nada mais é que a componente vertical da velocidade em
Mas quem vai ser o Ou seja, o raio de giração?
Vai ser a hipotenusa do triângulo maior da figura. Como é o cateto adjacente, teremos: