O pequeno bloco movimenta-se com velocidadeconstante na trajetória circular de raio sobre a superfície inclinada. Se no instante , determine as componentes , e da velocidade e da aceleração como funções do tempo.
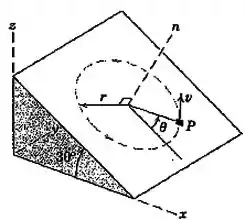
Passo 1
Opa, essa é uma questão que assusta a primeira vista, né?
Veja bem: ele tá te pedindo as componentes e da aceleração e velocidade daquele móvel. Porém, e você deve ter percebido, o móvel está executando uma trajetória em um plano inclinado.
E agora?
É só usarmos os novos eixos e :
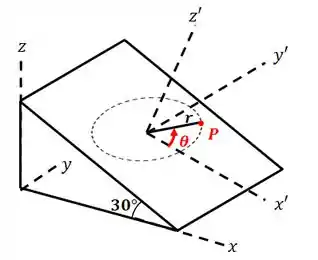
Depois a gente vai usar relações trigonométricas pra transferir o que calcularmos para as coordenadas retangulares padrão.
Além disso, veja que, pelo o enunciado, a velocidade tangencial vale . Assim, a velocidade angular vai ser:
E
Guarde no coração, vamos usá-las no final.
Passo 2
Beleza, nesse novo sistema de coordenadas, vamos ter:
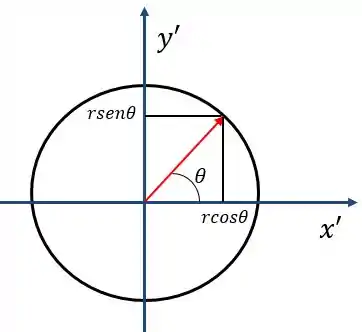
Assim:
E é nulo nesse novo sistema de coordenadas. Esse sistema está em cima do plano inclinado. Assim, a componente é nula.
Assim:
Perceba que usamos a regra da cadeia ali.
E:
Passo 3
Vamos como vamos decompor essas componentes na direção agora. Dê uma olhada na figura abaixo:
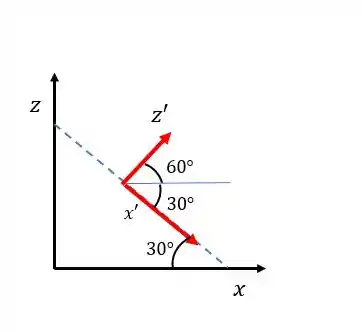
A linha azul tracejada indica o plano inclinado.
Bom, assim, teremos que decompor tanto o eixo quanto o . Assim:
Substituindo:
Substituindo
E Vai ser parecido, mas vamos ter uma subtração, já que as projeções terão sentidos opostos:
Faltou o . O que fazemos com ele? Nada, . O plano inclinado não influencia a direção pois ela é perpendicular a ele:
Passo 4
Tudo pronto, agora só falta a gente derivar pra achar
E:
E:
E:
E o
E:
E: