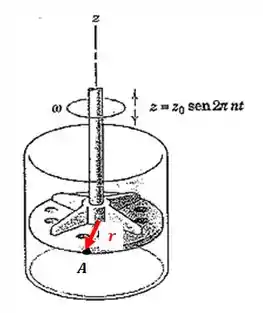
O elemento giratório em uma câmara de mistura recebe um movimento axial periódico enquanto está girando na velocidade angular constante . Determine a expressão para o módulo máximo da aceleração de um ponto sobre a borda de raio . A frequência da oscilação vertical é constante.
Passo 1
Vamos usar as coordenadas polares ( neste exercício.
Perceba que existe aceleração em Sim, a aceleração de um movimento harmônico.
E em Não! Perceba que o movimento circular ao redor do eixo de giro é feito sob uma velocidade constante.
Existe aceleração no sentido radial? Sim, como é um movimento circular, vai existir uma aceleração centrípeta.
Passo 2
Desenhando:
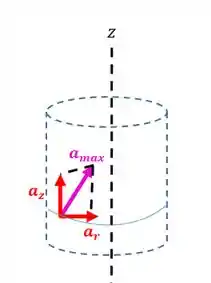
Passo 3
Vamos equacionar agora:
Perceba que o raio não varia, assim: Então:
E:
Como já discutimos.
E:
Show? Só derivamos duas vezes o movimento harmônico que tá rolando na vertical.
Passo 4
Assim, o módulo da aceleração é dado por:
E qual será o módulo máximo? Ocorrerá quando . Assim: