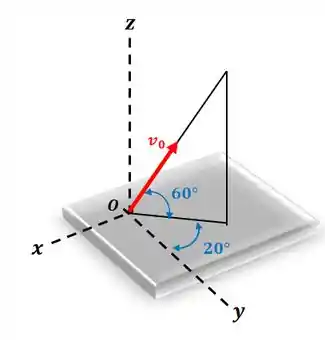
Um projétil é lançado a partir do ponto com uma velocidade inicial de módulo , direcionado como indicado na figura. Calcule as componentes , e da posição, velocidade e aceleração segundos após o lançamento. Despreze o arrasto aerodinâmico.
Passo 1
Perceba o seguinte: a velocidade de lançamento faz um ângulo de com o plano (horizontal). Já no plano , a velocidade faz um ângulo de com o eixo , no sentido negativo de
Vamos desenhar separadamente:
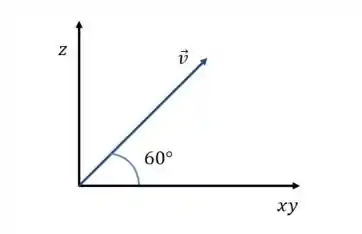
E:
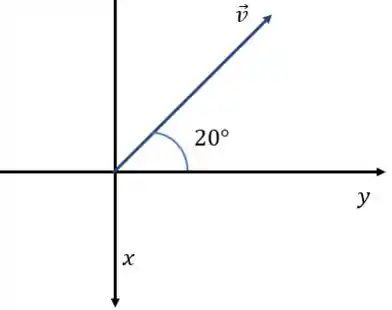
Beleza?
O que podemos concluir já de cara?
Bom, não é dito no enunciado, mas esse sistema está sendo influenciado pela gravidade local. Essa gravidade atua no eixo .
Sendo assim, o movimento do corpo será acelerado na direção , mas será um movimento de velocidade constante tanto em quanto em
Passo 2
Vamos primeiro calcular as equações gerais da posição, velocidade e aceleração para cada direção e depois calculamos para
Para
Onde
E:
Assim:
Substituindo os valores:
Dê uma olhada aqui no triângulo:
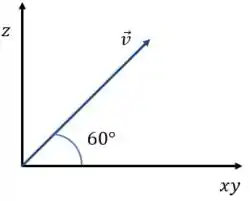
Beleza. E a posição vai ser dado por:
Já que a aceleração é constante e igual a
, já que ele parte da origem. Assim:
Passo 3
Agora vamos lidar com as posições e
Já que os movimentos terão velocidades constantes. Vamos olhar de novo a direção da nossa velocidade nesse plano:
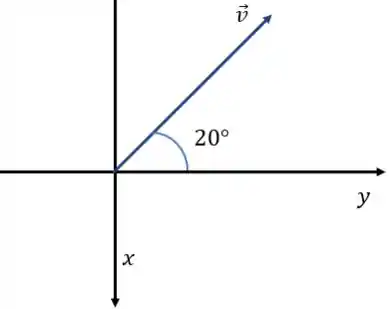
Beleza, mas eu posso pegar a velocidade que ele deu no enunciado ( e fazer:
e ?
Não!!!
Antes disso, precisamos calcular a componente horizontal de . A componente vertical é , que já calculamos. Assim, a horizontal será:
Agora sim:
E as equações do movimento?
Serão assim:
Onde:
E:
Então, vamos ter que:
E:
Passo 4
Assim:
Para
E:
Como:
E:
E também:
Então:
Formalizando isso vetorialmente:
E:
E para finalizar: