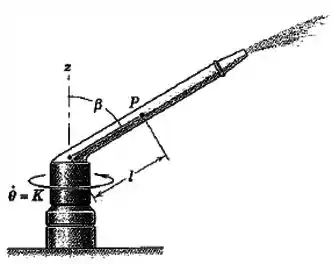
O esguicho rotativo borrifa uma grande área circular e gira com a velocidade angular constante . Partículas de água deslocam-se ao longo do tubo em uma taxa constante em relação ao tubo. Escreva expressões para os módulos da velocidade e aceleração de uma partícula de água para uma determinada posição no tubo rotativo.
Passo 1
Bom, o que está acontecendo ali é que essa mangueira está esguichando água enquanto gira.
Sua missão é encontrar as expressões para a velocidade da partícula e para a sua aceleração.
Bora?
Basicamente vamos identificar as variáveis importantes e aplicar as fórmulas.
Passo 2
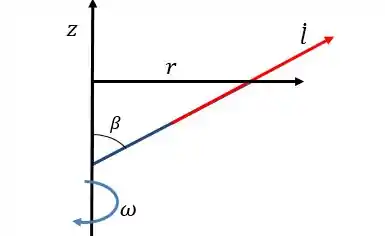
é a taxa de variação do deslocamento da partícula na direção de Temos, então, que a velocidade radial de uma partícula será dada por:
Sendo
E
E a velocidade em Será:
Percebeu que decompomos ali o pra achar
Assim, o módulo da velocidade será:
Passo 3
Para as acelerações, teremos:
A variação de , que nada mais é que a variação de , é constante, assim:
E:
E:
Só que , já que , que é uma constante. Assim:
E só falta
Assim, o módulo da aceleração será dado por: