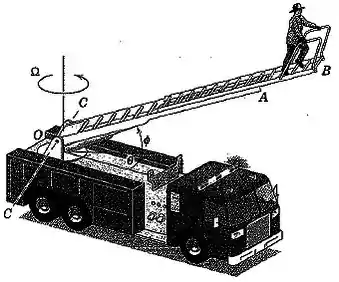
A estrutura de base da escada de um carro de bombeiros gira em torno de um eixo vertical através de com uma velocidade angular constante . Ao mesmo tempo, a unidade da escada se eleva a uma taxa constante , e a seção da escada se prolonga de dentro da seção na taxa constante de . No instante em questão, , e Determine o módulo da velocidade e da aceleração da extremidade da escada.
Passo 1
Vamos usar as coordenadas esféricas aqui.
Primeiro, vamos calcular
E:
E só falta:
Assim:
Passo 2
Em relação às acelerações:
E:
Assim:
Assim:
Resposta
Exercícios de Livros Relacionados
Um brinquedo de parque de diversões chamado “saca-rolha” leva os passageiros de cabeça para baixo através da curva de uma hélice cilíndrica horizontal. A velocidade dos carros quando passam pela posiç
Uma aeronave decola em A e se eleva em um ângulo constante com inclinação de 1 para 2 no plano vertical y - z com uma velocidade constante v = 400k m / h . A aeronave é rastreada por radar em O . Para
Na parte inferior de uma acrobacia aérea na qual o avião descreve um círculo no plano vertical x - y a uma altitude de 400m , o avião tem uma velocidade de 600k m / h sem aceleração horizontal x . O r
A partícula P se desloca para baixo na trajetória espiral que está enrolada ao redor da superfície de um cone circular reto com raio de base b e altura h . O ângulo γ entre a tangente à curva em qualq
14.39 Em um jogo de bilhar, a bola A se desloca com uma velocidade v0 de intensidade v0 5 m/s quando ela atinge as bolas B e C, que se encontram em repouso e alinhadas como mostrado na figura. Sabendo