A figura abaixo representa um disco homogêneo e uniforme, de espessura desprezível, e raio R. O disco gira no sentido horário em torno do seu eixo de simetria, com velocidade angular constante de módulo , e cai sob a ação do campo gravitacional próximo à superfície da Terra, mantendo-se sempre num mesmo plano vertical.
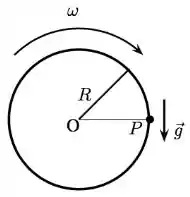
Sabendo-se que a aceleração do centro de massa do disco é igual a , a aceleração da gravidade, pode-se concluir que o módulo da aceleração do ponto P localizado na borda do disco, mostrado na figura, é:
Passo 1
Parece complicado né? Mas calma, vamos ver rapidinho primeiro como o ponto se comporta durante os dois movimentos combinados: a queda e a rotação:
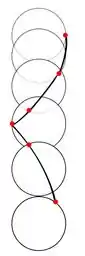
Agora vamos ver separadamente os dois movimentos:
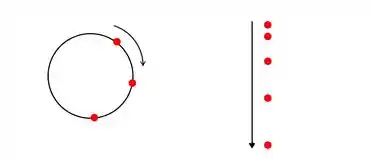
Veja que se o disco estivesse caindo sem rodar, a bolinha vermelha, que representa o nosso ponto , iria cair em linha reta e se o disco rodasse sem cair, o ponto iria simplesmente girar.
A gente conhece a aceleração do ponto para cada um dos movimentos separados não é mesmo? Veja:
Bem, se o movimento do ponto tem uma trajetória combinada, pra cada ponto dessa trajetória então podemos considerar que as duas acelerações acima existem! Vamos ter então que a aceleração no ponto vai ter essa expressão simpática:
Sendo assim, o módulo da aceleração vai ser: