Uma barra de aço AB e CD estão conectadas por duas engrenagens (E e F). A barra AB sofre a ação de um motor que transfere a ela uma potência de 50 HP a uma frequência de 180RPM. Sabendo que as dimensões de cada barra, assim como os diâmetros das engrenagens são dados na figura, determine a tensão cisalhante máxima ao qual a barra CD estará sujeita.
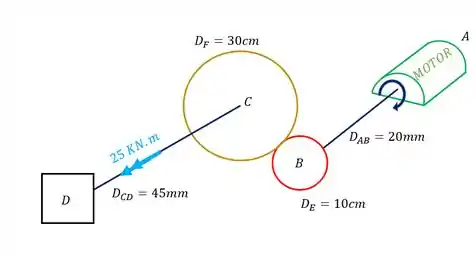
Passo 1
Nosso objetivo é determinarmos a tensão cisalhante na barra CD, mas antes dela temos muita coisa pra analisar. O nosso objetivo então é o seguinte, é trocar tudo que vem antes da barra CD por um toque equivalente a isso tudo, mas sempre respeitando as regras que temos que usar, basicamente o nosso objetivo é chegar nesse caso
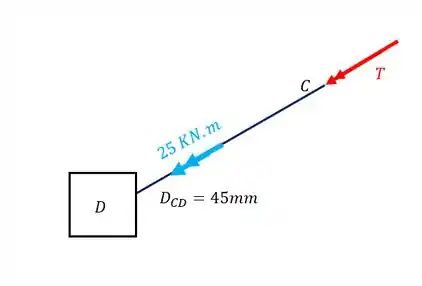
Quando chegarmos nessa situação usaremos a nossa fórmula para determinar o cisalhante máximo que é dado por
Mas para chegarmos nessa situação precisamos seguir um passo a passo.
Passo 2
Primeiro temos que nos livrar do nosso motor, ou seja, precisamos trocar o nosso motor por um torque equivalente no sentido mostrado na figura. Sabemos pela teoria que a fórmula que nos fornece isso é dada por
Em que é a potência do nosso motor e a frequência, ou seja, devemos nos precaver com o que se relaciona com as unidades. Então vamos lá.
Primeiro sabemos que a potência do nosso motor é dada por
Devemos ter na cabeça a conversão dessa unidade, alguns professores não gostam de dar esse valor na prova, então a nossa relação é
Convertendo teremos que
Também devemos ver a nossa frequência que é dada por
Se dividirmos esse valor por 60 acharemos a nossa frequência em Hz, além do mais, RPM são rotações por minutos, e Hz por segundo, logo fazendo a conversão teremos que
Agora que já temos os nossos valores basta substituir na nossa equação principal
Então a nossa figura agora será
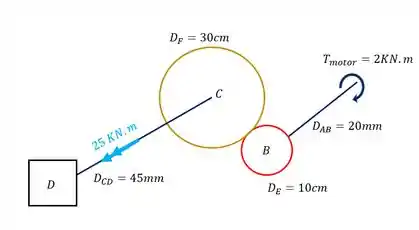
Passo 3
Para trocarmos a nossa barra AB é muito simples, se não há nela nenhum esforço torsor além do transferido pelo motor, significa que todo o esforço transferido pelo motor será transferido para a engrenagem E, como mostra a nossa figura.
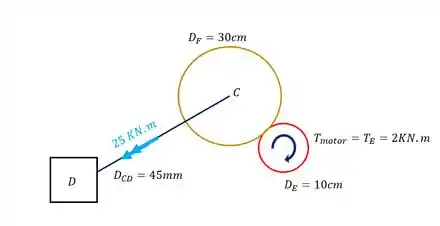
Passo 4
Agora temos que tomar cuidado pois se trata de uma relação entre engrenagens, se olharmos elas separadamente teremos o seguinte
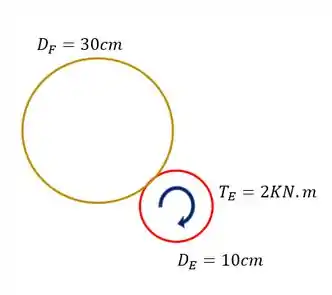
A primeira coisa que devemos saber é que, se a engrenagem E gira no sentido horário, então a engrenagem F girará no sentido anti-horário, da mesma forma ocorreria se os sentidos fossem invertidos, logo sabemos que os sentidos de giro serão
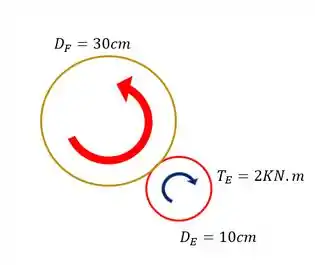
Agora que já sabemos os sentidos de giro precisamos analisar as nossas engrenagens separadamente
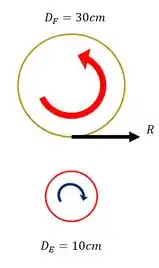
Sabemos que a engrenagem E empurra a engrenagem F com uma força R mostrada na figura, o que faz com que a engrenagem F gire.
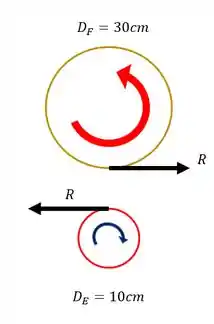
Sabemos também que pela terceira lei de newton aparecerá uma reação na engrenagem E, como o mostrado na figura acima.
Mas no que essas forças nos ajudam?
Sabemos que para calcularmos o torque nessas engrenagens, basta multiplicarmos a força pelo raio
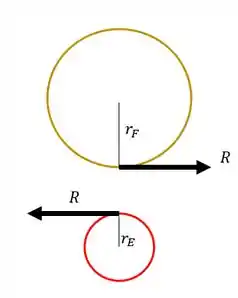
Para cada engrenagem teremos que
Como sabemos que o valor de R é igual pela lei da ação e reação teremos que
Igualando
Como nosso objetivo é determinar o valor de iremos isola-lo na fórmula
Substituindo teremos que
Substituindo na nossa fórmula teremos que
Olhando a nossa figura termos que o nosso torque está agindo da seguinte forma
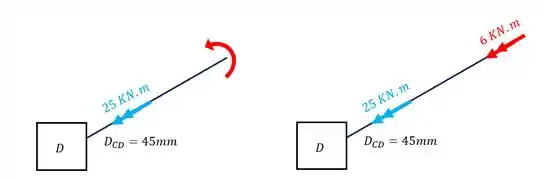
Onde enfim chegamos no objetivo inicial que tínhamos. Trocamos o Motor, a barra AB e as engrenagens E e F pelo nosso torque de 6KN.m.
Passo 5
Agora que já temos a nossa barra apenas precisamos analisar a nossa fórmula para tensão cisalhante máxima.
Primeiro sabemos que o cisalhante máximo é o ponto mais externo da nossa barra, ou seja
Também sabemos que o momento polar de inercia para seções circulares é dada por
Substituindo teremos que
Sabemos que
Falta ainda calcularmos o valor do torque.
Passo 6
Para calcularmos o torque precisamos dividir a nossa barra em dois pontos e ver em qual dos dois o torque será maior, como queremos o cisalhante máximo, usaremos o torque máximo.
Fazendo o diagrama de corpo livre teremos que
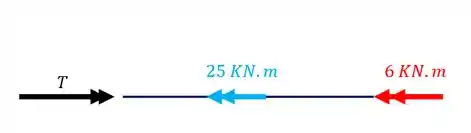
Fazendo o equilíbrio teremos que
Fazendo os dois cortes teremos que
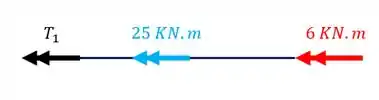
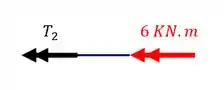
Então sabemos que devemos usar o maior valor para o cálculo
Passo 7
Substituindo os valores que encontramos teremos que