Exercícios Resolvidos de Potência e Torque

Enunciado

O eixo maciço de alumínio tem diâmetro de e tensão de cisalhamento admissível . Determine o maior torque que pode ser aplicado ao eixo se ele também estiver sujeito a outros carregamentos de torção. Exige-se que aja na direção mostrada. Determine também a tensão de cisalhamento máxima no interior das regiões e .

Passo 1

O que está acontecendo?

O eixo maciço de diâmetro , e, consequentemente, raio tem uma tensão de cisalhamento admissível .

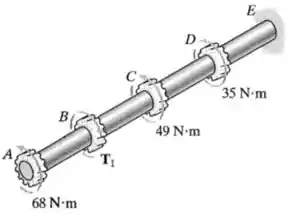
Fazendo um diagrama de corpo livre desse eixo (usando a regra da mão direita!), vemos os torques nos pontos , , e desse eixo, assim como a reação que surge no ponto :

Por causa desses diferentes torques, os diferentes trechos do eixo vão estar resistindo à diferentes torques internos.

E o que é que o exercício quer?

Ele quer saber o maior torque que pode ser aplicado no eixo.

O maior torque que pode ser aplicado é aquele que ainda garante que a tensão de cisalhamento máxima absoluta no eixo seja menor ou igual à admissível:

Então para resolver esse exercício, vamos:

1. Identificar a intensidade do maior torque interno sofrido pelo eixo, em função do torque aplicado.

& 2. Desenvolver a condição de projeto usando a fórmula da torção e isolar o torque desconhecido na expressão que for obtida.

Em seguida, o exercício ainda quer que a gente use o valor encontrado para para determinar a tensão de cisalhamento máxima no interior das regiões e .

Para isso, vamos usar, mais uma vez, a fórmula da torção.

Passo 2

Então vamos começar identificando a intensidade do maior torque sofrido pelo eixo.

Para tanto, precisamos fazer uma análise dos esforços internos no eixo.

Essa análise até pode ser feita de cabeça, mas alguns professores ainda requerem que ela seja feita no papel.

Então vamos lá!

Começamos a análise observando os esforços internos nas diferentes seções do eixo:

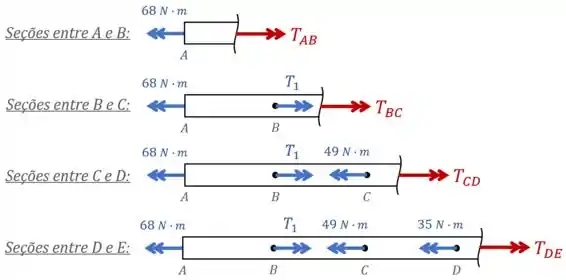
Nessa análise, desenhamos os torques internos em vermelho “saindo” da peça pois essa é a nossa convenção.

Caso os seus professores utilizem a convenção contrária (a de que os torques internos são positivos quando “entram” nas peças), você deve desenhar os torques internos entrando.

Feito isso, aplicamos as condições de equilíbrio para cada uma das situações acima.

Nesse caso, a única condição de equilíbrio aplicável é o equilíbrio de torques:

Aplicando ele para cada caso, temos que:

Em seguida, isolando os torques em cada trecho, encontramos que:

Considerando que deve possuir um valor grande, podemos assumir que vai possuir uma intensidade maior que a intensidade de .

Assim, concluímos que a intensidade do maior torque sofrido pelo eixo é:

Passo 3

Em seguida, podemos desenvolver a nossa condição de projeto:

Aqui, temos que é a tensão de cisalhamento máxima absoluta.

Dessa forma, deve ser calculada usando a fórmula da torção e a intensidade do maior torque sofrido pelo eixo.

Sendo assim, temos que:

Substituindo isso na nossa condição de projetos, ela fica assim:

Em seguida, observamos que o momento polar de inércia do eixo maciço vai ser dado pela fórmula , de tal forma que:

Simplificando tudo, isso fica assim:

Isolando , temos que:

E substituindo:

;
& ,

Encontramos que:

Como estamos trabalhando com , reescrevemos o resultado acima nessa unidade:

E finalmente, usando que , encontramos que:

Ou seja, o maior torque que pode ser aplicado é:

Passo 4

Resolvida a parte principal do exercício, agora vamos calcular os outros dois valores pedidos pelo exercício:

A tensão de cisalhamento máxima para a região do eixo;
E a tensão de cisalhamento máxima para a região .

Nesses dois casos, vamos usar a fórmula da torção:

Usar que o momento polar de inércia de um eixo maciço é :

E simplificar tudo para encontrar que:

Aplicando a fórmula acima para a região , temos que:

As barras de módulo são colocadas em volta do torque uma vez que esse torque vai ter um valor negativo, mas o cálculo de não se importa com os sinais do torque.