O projeto prevê que o eixo de transmissão de um automóvel será um tubo de parede fina. O motor transmite quando o eixo está girando a . Determine a espessura mínima da parede do eixo se o diâmetro externo for . A tensão de cisalhamento admissível do material é .
Passo 1
O que está acontecendo?
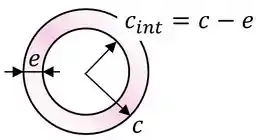
O eixo tem um diâmetro externo , e, consequentemente um raio externo .
Além disso ele não é maciço.
Ao invés disso, ele é feito de uma parede fina de espessura , de tal forma que ele possui um raio interno :
O eixo transmite uma potência a uma frequência , de tal forma que ele tem que suportar um torque :
E, por fim, o material do eixo possui uma tensão de cisalhamento admissível .
E o que é que o exercício quer?
Ele quer saber a espessura mínima da parede do eixo para que o torque transmitido não gere nele uma tensão de cisalhamento máxima maior que a admissível:
Sendo que essa tensão pode ser expressa pela fórmula da torção:
Onde é o momento polar de inércia do eixo e é dado pela fórmula abaixo para um eixo de seção vazada com raio externo e raio interno :
Passo 2
Antes de qualquer coisa, vamos converter as unidades da frequência para o sistema internacional.
Do enunciado, temos que:
Mas como , temos que:
O que significa que:
Passo 3
Agora sim, já temos tudo o que precisamos para pegar a condição de projeto e desenvolvê-la até encontrar a espessura mínima necessária para a parede do eixo.
Aplicando a condição de projeto, temos:
E em seguida, aplicando a fórmula da torção, temos que:
Substituindo a fórmula do momento polar de inércia para um eixo vazado e a fórmula do torque , isso fica assim:
Arrumando tudo, temos que:
Aqui, percebemos a necessidade de uma mudança de planos. 🤔
A ideia era substituir e isolar a espessura para encontrar seu valor mínimo.
Mas com a existência da potência no raio interno , fazer isso seria muito complicado.
Então vamos aceitar só encontrar o raio interno máximo possível por enquanto.
Daí, com o valor que encontrarmos, vamos usar que para calcular a espessura mínima necessária para o nosso eixo!
Passo 4
Partir isolar então para encontrar seu valor máximo possível!
Para tanto, começamos passando o termo para a direita:
E, em seguida, passamos para a esquerda:
Finalmente, isolamos :
Para encontrarmos que o valor máximo possível para é:
Substituindo nessa expressão:
- ;
- ;
- & ,
Encontramos que:
O que dá:
Passo 5
Agora que temos o máximo valor possível para , podemos encontrar o valor mínimo necessário para .
Aplicando que:
Isolando :
E substituindo:
- ;
- & ,
Encontramos que:
O que dá a nossa resposta: