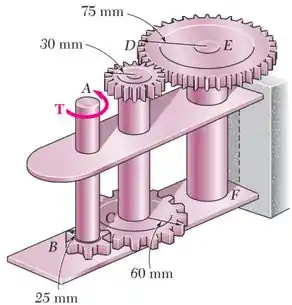
Um torque de intensidade é aplicado ao eixo do trem de engrenagem mostrado. Sabendo que a tensão de cisalhamento é de em cada um dos três eixos sólidos, determine o diâmetro necessário para o eixo , o eixo e o eixo .
Passo 1
O que está acontecendo?
Os eixos , e são maciços, possuindo:
- diâmetros , e ;
- E, consequentemente, raios .
Já as engrenagens , , , e possuem raios , , e , respectivamente.
E um torque é aplicado ao eixo .
Para descobrir o torque que é gerado nos demais eixos, é preciso perceber que o torque em uma engrenagem é igual à força que é aplicada nos dentes dela vezes o raio dela:
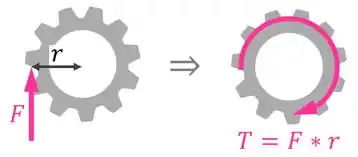
Assim, é possível dizer que:
E pelo princípio da ação e reação, é possível dizer que as forças que uma engrenagem faz na outra são iguais, de tal forma que, para as engrenagens e , por exemplo:
E o que é que o exercício quer?
Ele quer saber o diâmetro de cada um dos eixos para que a tensão máxima de cisalhamento neles seja igual à .
Para resolver o exercício, vamos primeiro encontrar o torque aplicado em cada engrenagem e em cada eixo.
Em seguida, vamos poder definir a tensão máxima de cisalhamento em cada eixo e descobrir o diâmetro necessário para cada eixo para que .
Passo 2
Então vamos começar encontrando o torque em cada engrenagem e em cada eixo do problema.
Primeiro, para o eixo , que gira junto com a engrenagem , sabemos que é aplicado nele um torque , de tal forma que:
Agora, devido às forças exercidas entre as engrenagens e , temos que:
O que significa que:
Substituindo , e , isso nos diz que:
Assim, para o eixo , temos que:
E devido às forças exercidas entre as engrenagens e , temos que:
O que significa que:
E substituindo , e , isso nos diz que:
E assim, para o eixo , temos que:
Passo 3
Agora, podemos definir a tensão máxima de cisalhamento para cada eixo.
Primeiro, sabemos que vai ser dada pela fórmula da torção:
E também sabemos que todos os eixos são maciços, de tal forma que .
Sendo assim, temos que:
Simplificando, isso fica assim:
E, como, em todos os casos, estamos querendo descobrir o diâmetro dos eixos, e não os raios , podemos fazer a substituição :
E arrumando tudo, isso fica assim:
Ainda podemos isolar o diâmetro dos eixos nessa equação para encontrar que:
Agora, só falta aplicar a equação acima para cada eixo e substituir sempre .
Passo 4
Começando pelo eixo , para resolver o item , temos que:
Substituindo:
- ;
- & ,
- ;
- & ,
- ;
- & ,
Encontramos que:
Seguindo com o eixo , para resolver o item , temos que:
Substituindo:
Encontramos que:
E finalizando com o eixo , para resolver o item , temos que:
Substituindo:
Encontramos que: