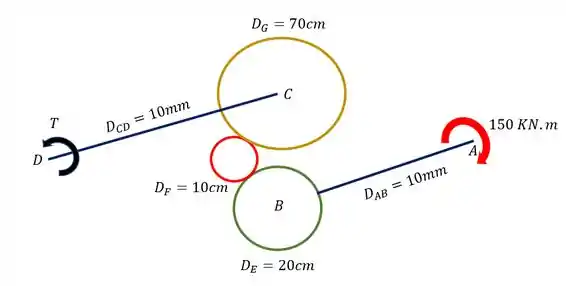
Uma barra sofre uma torção mostrada na figura. Sabendo que essa torção foi dada na barra AB, determine qual deve ser o torque resistente na barra CD para que essa barra não sofra movimento. Os valores de diâmetro das engrenagens (E, F e G) e das barras é dado na própria figura.
Passo 1
Para resolvermos esse exercício, precisamos fazer o torque que foi aplicado na barra AB, chegue na barra CD, só assim poderemos fazer o equilíbrio e saber qual será o torque que manterá o sistema parado. Vamos então ir trocando as nossas peças.
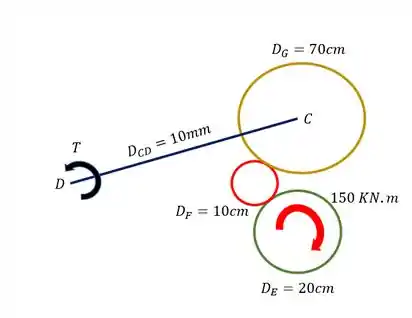
Começaremos tirando a nossa barra AB. Como ela não possui nenhum torque aplicado no comprimento dela, tendo apenas o inicial de intensidade , podemos transferir esse torque e esse sentido diretamente para a engrenagem E, olhando a nossa figura teremos que
Passo 2
Agora temos que tomar cuidado pois se trata de uma relação entre engrenagens, se olharmos elas separadamente teremos o seguinte
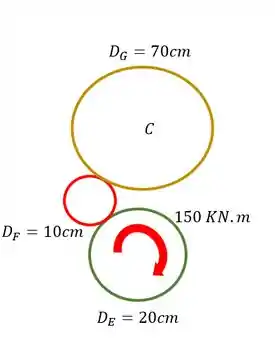
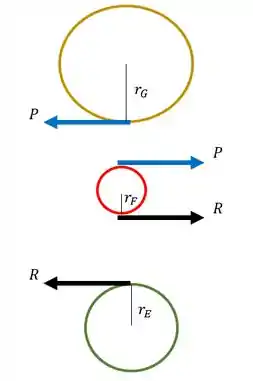
A primeira coisa que devemos saber é que, se a engrenagem E gira no sentido horário, então a engrenagem F girará no sentido anti-horário, da mesma forma se a engrenagem F gira no sentido anti-horário então a engrenagem G gira no sentido horário, sendo o mesmo princípio que ocorreria se os sentidos fossem invertidos, logo sabemos que os sentidos de giro serão
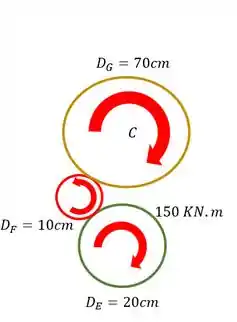
Agora que já sabemos os sentidos de giro precisamos analisar as nossas engrenagens separadamente
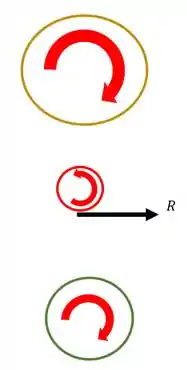
Sabemos que a engrenagem E empurra a engrenagem F com uma força R mostrada na figura, o que faz com que a engrenagem F gire.
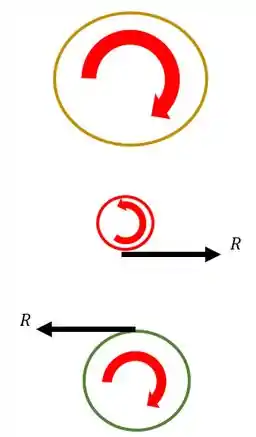
Sabemos também que pela terceira lei de newton aparecerá uma reação na engrenagem E, como o mostrado na figura acima.
Também sabemos que como a engrenagem F está acoplada na engrenagem G então está também aplicara uma força P na engrenagem G
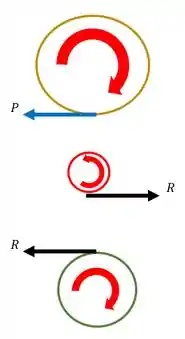
E da mesma forma, pela lei da ação e reação teremos uma reação na engrenagem F como mostra a figura
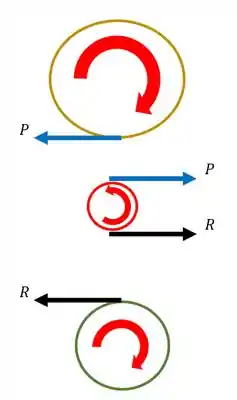
Mas no que essas forças nos ajudam?
Sabemos que para calcularmos o torque nessas engrenagens, basta multiplicarmos a força pelo raio
Para cada engrenagem teremos que
Como temos duas fórmulas para , podemos concluir que P=R
Como sabemos que o valor de R é igual pela lei da ação e reação teremos que
Igualando
Também teremos que
Como já sabemos que as forças são iguais, então podemos fazer a relação de engrenagens como
Como nosso objetivo é determinar , podemos fazer isso diretamente, ou por partes. Fazendo primeiro por partes teremos que
E em seguida faremos
Ou podemos fazer diretamente
sabemos que
Fazendo por partes teremos que
Em seguida faremos
Para conferir faremos também o cálculo direto
Oque comprova que a relação está correta.
Olhando a nossa figura termos que o nosso torque está agindo da seguinte forma
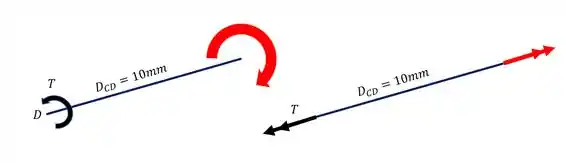
Onde enfim chegamos no objetivo inicial que tínhamos. Trocamos a nossa barra AB e as nossas engrenagens pelo nosso torque de 525KN.m.
Passo 3
Como nosso objetivo é determinar o valor do torque em D para que não ocorra movimento teremos que
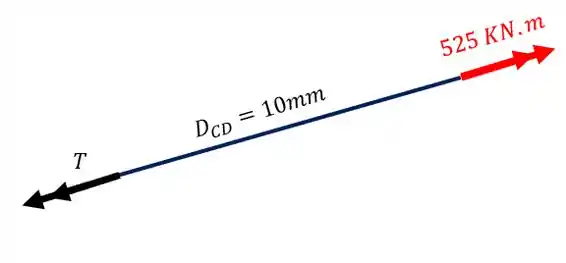
Fazendo o equilíbrio da nossa peça teremos que