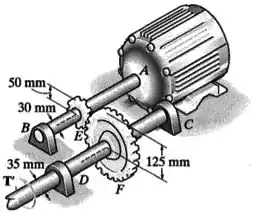
O motor transmite um torque de ao eixo . Esse torque é transmitido ao eixo pelas engrenagens em e . Determine o torque de equilíbrio no eixo e a tensão de cisalhamento máxima em cada eixo. Os mancais , e permitem a livre rotação dos eixos.
Passo 1
O que está acontecendo?
O motor transmite um torque ao eixo , que é maciço e possui um diâmetro , e, consequentemente, um raio .
Já o eixo também é maciço, mas possui um diâmetro , e, consequentemente, um raio .
E as engrenagens e possuem raios e .
Para saber torque que é gerado no eixo , é preciso perceber que o torque em uma engrenagem é igual à força que é aplicada nos dentes dela vezes o raio dela:
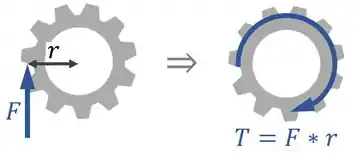
Assim, podemos dizer que:
E pelo princípio da ação e reação, é possível dizer que as forças que uma engrenagem faz na outra são iguais, de tal forma que, para as engrenagens e , temos que:
Mas a engrenagem faz parte do eixo , que gira com o torque , de tal forma que .
E a engrenagem faz parte do eixo , que gira com um torque desconhecido, de tal forma que .
Dessa forma, temos que:
O que significa que:
E o que é que o exercício quer?
Primeiro, ele quer que a gente encontre o torque de equilíbrio no eixo , que pode ser encontrado através da equação acima.
Depois, ele quer que saber a tensão de cisalhamento máxima em cada eixo, que pode ser encontrada aplicando a fórmula da torção abaixo para o eixo e para o eixo :
Passo 2
Então vamos começar encontrando o torque de equilíbrio no eixo pela relação de engrenamento:
Substituindo:
- ;
- ;
- & ,
Encontramos que:
O que dá:
Passo 3
Agora, vamos calcular as tensões de cisalhamento máxima em cada eixo.
Aplicando a fórmula da torção para o eixo , que está submetido a uma torção , temos:
Como o eixo é maciço, seu momento polar de inércia vai ser dado pela fórmula .
Dessa forma, temos que:
Simplificando, isso fica assim:
Finalmente, substituindo:
- ;
- & ,
- ;
- & ,
Encontramos que:
E, como é o mesmo que , isso significa que:
Já aplicando a fórmula da torção para o eixo , que está submetido a um torque , temos:
Mais uma vez, o eixo é maciço, então seu momento polar de inércia vai ser dado pela fórmula :
Simplificando, temos:
Por fim, substituindo:
Encontramos que: