Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Potência em Circuito CA

Ver Teoria
Exercício 91234567810

Enunciado

Calcule o valor eficaz da forma de onda de corrente abaixo e a potência média liberada para um resistor de 12   Ω , quando a corrente percorre o resistor.

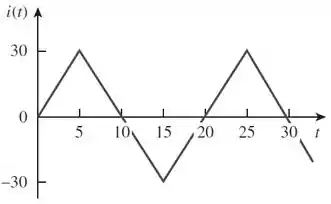
Passo 1

Primeiro temos que encontrar a expressão de i ( t ) . Analisando a onda vemos que seu período é 20 . Logo:

T = 20

Para facilitar a nossa análise, vamos encontrar a expressão para corrente no intervalo 5 < t < 25 .

No intervalo 5 < t < 15 a forma de onda da corrente é uma reta decrescente. Sabemos que a equação de uma reta qualquer é:

y = a x + b

No nosso caso, y = i e x = t , logo:

i = a t + b

Vamos encontrar a e b , escolhendo dois pontos nesse intervalo. O primeiro ponto será:

P 1 = ( t = 5 ; i = 30 )

Substituindo na equação da reta:

30 = a 5 + b

5 a + b = 30       ( 1 )

Fazendo a mesma coisa para P 2 = ( t = 10 ; i = 0 ) , temos

0 = a 10 + b

10 a + b = 0       ( 2 )

Passo 2

Fazendo a equação ( 1 ) menos a ( 2 ) , temos:

- 5 a = 30

a = - 6

Substituindo o valor de a na equação ( 2 ) :

10 - 6 + b = 0

b = 60

Então, a expressão para corrente no intervalo 5 < t < 1 5 é:

i t = - 6 t + 60

Passo 3

Agora, vamos fazer a mesma coisa para encontrar a expressão da corrente para o intervalo 15 < t < 25 .

O primeiro ponto é P 1 = ( t = 1 5 ; i = - 30 ) . Substituindo na equação da reta:

- 30 = a 15 + b

15 a + b = - 30       ( 3 )

Agora para P 2 = ( t = 25 ; i = 30 ) :

30 = a 25 + b

25 a + b = 30       ( 4 )

Fazendo a equação ( 3 ) menos a ( 4 ) , temos:

- 10 a = - 60

a = 6

Substituindo o valor de a na equação ( 4 ) :

25 6 + b = 30

b = 30 - 150

b = - 120

Então, a expressão para corrente no intervalo 1 5 < t < 25 é:

i t = 6 t - 120

Passo 4

Agora que temos a expressão da corrente para todo o período é só jogar na fórmula e calcular o valor RMS:

I R M S = 1 T ∫ 0 T i 2   d t

I R M S = 1 20 ∫ 5 15 ( - 6 t + 60 ) 2   d t + ∫ 15 25 6 t - 120 2   d t  

I R M S = 1 20 ∫ 5 15 ( 36 t 2 - 72 0 t + 3600 )   d t + ∫ 15 25 ( 36 t 2 - 1440 t + 14400 )   d t  

I R M S = 1 20 36 t 3 3 - 720 t 2 2 + 3600 t 15 5 + 36 t 3 3 - 1440 t 2 2 + 14400 t 25 15  

I R M S = 1 20 13 500 - 10 500 + 9 7 500 - 94500  

I R M S = 1 20 3000 + 3000  

I R M S = 6 000 20  

I R M S = 300

I R M S = 17,32   A

Passo 5

Agora, precisamos encontrar a potência média liberada no resistor de 12   Ω quando essa corrente percorre o resistor. Para isso, basta aplicar a formula abaixo:

P = R I R M S 2

Moleza, né?!

P = ( 12 ) × 17,32 2

P = 3599,8   W

Resposta

I R M S = 17,32   A

P = 3599,8   W

Exercícios de Livros Relacionados

7. Dado o circuito da figura 11.39 , determine a potência média absorvida pelo resistor de 10Ω .
8. No circuito da figura 11.40 determine a potência média absorvida pelo resistor de 40Ω .
6. Para o circuito da figura 11.38 , i s = 6 cos ⁡ 10 3 tA . Determine a potência média absorvida pelo resistor de 50Ω .
3. Uma carga é formada por um resistor de 60Ω em paralelo com um capacitor de 90m F . Se a carga for conectada a uma fonte de tensão v s t = 160 cos ⁡ 2000 t , determine a potência média liberada para
29- Calcule o valor eficaz da forma de onda da corrente mostrada na Figura 11.60 e a potência média liberada para um resistor de 12Ω , quando a corrente percorre o resistor.